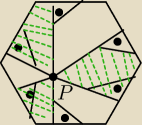
wielokąt Halston: Dany jest dowolny wielokąt foremny z parzystą liczbą boków i dowolny punkt wewnątrz niego. Wykaż ze suma pol "zielonych figur" jest dwa razy mniejsza niż pole całego wielokąta.

kerajs: To nieprawda. Narysuj sobie kwadrat, a punkt wybierz blisko jednego z wierzchołków. PS Moim zdaniem zielone figury powinny być trójkątami o jednym z boków będących bokami wielokąta.

Halston: Dzięki przeanalizuję to.

Halston: Sorry n=6,8,10,12... czyli liczba boków większa bądź równa 6, więc problem nadal otwarty

wredulus_pospolitus: a na jakiej zasadzie ów 'zielone figury' powstają

Halston: Z punktu P pod kątem prostym do każdego boku są prowadzone odcinki. Wtedy otrzymujemy czworokąty.

falo: Tu też

kerajs: To nieprawda. Narysuj sobie dowolny ''wielokąt foremny z parzystą liczbą boków'', a punkt wybierz blisko jednego z wierzchołków. A jeśli taki wybór nie jest możliwy ze względu na konieczność pojawienia się czworokątnych ''zielonych figur'', to nieprawdą jest, że zależność zachodzi dla dowolnego punktu wewnątrz wielokąta. PS Możliwe, iż przy zmienionej treści coś tam można wykazać, lecz przy aktualnej jest to niemożliwe.

Halston: Jednak punkt P nie jest dowolny, tylko taki aby możliwe było ze pojawienie się czworokątnych ''zielonych figur''