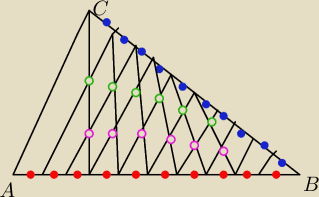
trójkaty Halston: Boki trójkąta CB i AB podzielono na dziesięć równych części. Wykaz ze punkty "zielone" są współliniowe oraz punkty "różowe" też są współliniowe.

kerajs: Skoro odcinki na ramionach kąta są proporcjonalne , to sieczne kąta je wyznaczające są równoległe. Wszystkie trójkąty o podstawach z niebieską kropką i zielonym wierzchołkiem są przystające, więc przez zielone punkty przechodzi prosta równoległa do CB. Analogicznie jest z różowymi punktami.

Halston: Wielkie dzięki

an: Jeżeli to ma być zgodnie z rysunkiem to owszem są współliniowe, ale reszta wyjaśnienie z 21:56 to nie prawda

Halston: an właśnie trzeba pokazać że one są współliniowe

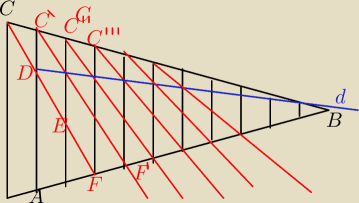
an: Przypomnij sobie twierdzenie Talesa A tak na "chłopski rozum" to CD=DE=EF; C'=E'=F' itd CC'=C'C"....=DD'=D'D"=...itd

C'D		C''D'
	=		=... itd
C"D'		C"'D''

czyli że "d" co jednakowy odcinek zbliża się jednakowo do CB, czyli jest pod stałym kątem, a więc jest prostą

an: Przedobrzyłem ta proporcja to oczywiście bzdura reszta się zgadza

an: można by C'D=C"D'+Δ; C''D'=C"'D"+2Δ ......

an: zaplątało się 2 C'D=C"D'+Δ; C''D'=C"'D"+Δ ..itd

Halston: Jeśli pole trójkąta przy wierzchołku B wynosi 3., to które trójkąty mają pola 3,4,5,6,7,8,9,10: https://zapodaj.net/images/8bcee0e42bb04.jpg

kerajs: ''an: (...) wyjaśnienie z 21:56 to nie prawda'' Fakt. O ile sieczne lewoskośne są równoległe (bo odcinane odcinki są proporcjonalne), to sieczne prawoskośne są nie są równoległe (bo odcinane odcinki są proporcjonalne prócz pierwszych od prawej). Sorry. .

Halston: A jak to zrobic?: Jeśli pole trójkąta przy wierzchołku B wynosi 3., to które trójkąty mają pola 3,4,5,6,7,8,9,10: https://zapodaj.net/images/8bcee0e42bb04.jpg

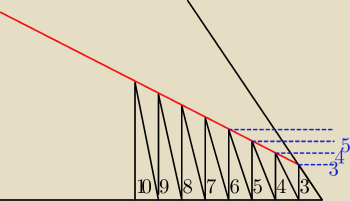
an: np. j/w podstawa każdego trójkąta 2 wysokość pierwszego 3 , każdy następny o 1 wyższy ich wierzchołki ułożą się współliniowo, natomiast na Twoim rysunku sama powierzchnia jednego trójkąta to za mało, i do czego Ci to potrzebne.