trapez Mirko: Rozważmy trapez równoramienny ABCD z AD=BC i AB<CD. Załóżmy, że odległości od wierzchołka A do BC, CD i BD wynoszą odpowiednio 15, 18 i 10. Oblicz pole ABCD.

an: Czy to jest dokładna sprawdź treść zadania.

am: Te dane wystarczą. Trzeba znaleźć trójkąty podobne, wyznaczyć związki między bokami tych trójkątów i w trójkątach prostokątnych zastosować tw. Pitagorasa

an: Problem polega na tym, że trapez o takich wymiarach nie istnieje

dlaczego: nie istnieje?

Mirko: an możesz wyjaśnić czemu nie istnieje

an: Istnieje coś mi się geogebra "namieszała" wynik to ≈400,93

Mirko: Jak policzyć to pole?

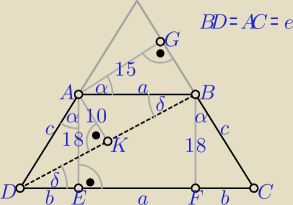
am: Bez wspomagaczy np Geogebrą a>0 i b>0 i c>0 i e>0

	15		18
ΔABG∼ΔADE ⇒		=		⇒ c = 1,2a
	a		c

	18		10
ΔDFB∼ΔAKB ⇒		=		⇒ e = 1,8a
	e		a

Pitagoras: ΔADE: b² + 18² = c² = 1,44a² i ADFB: (a + b)² + 18² = e² = 3,24a² ⇒ a² + 2ab + 1,44a² = 3,24a² stąd a = ..., b = ...

ak:

Mirko: Dzieki

Saizou : Eta

am: Saizou, Ecie oczywiście należą się brawa i