Optymalizacja Raksi: Z drutu o długości 120 dm wykonano szkielet graniastosłuipa prostego, którego jedna z krawędzi podstawy jest o 6 dm krótsza od drugiej. Do tego szkieletu przymocowano metalowe płyty, dzięki czemu powstało pudło z górnym wiekiem. Oblicz największe możłiwe koszty wyprodukowania takiego pudła, gdzie − 1 dm drutu kosztuje 4 zł, − 1 dm² metalowej płyty kosztuje 18 zł (inne koszty pomijamy).

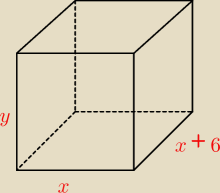
wredulus_pospolitus: 2*(x + x+6) + 4y = 120 −−−> 4x + 4y = 108 −−−> x + y = 27 −−−> y = 27 − x P_płyt = 2*x*y + 2*(x+6)*y + x*(x+6) = 2*x*(27−x) + 2*(x+6)*(27−x) + x*(x+6) masz funkcję P(x). Liczysz pochodną ... szukasz ekstremum i po krzyku Pamiętaj o ZAŁOŻENIACH odnośnie 'x'

Raksi: Z własności funkcji kwadratowej też można skorzystać?

wredulus_pospolitus: jak chcesz szukać wierzchołka paraboli ... to też możesz

Raksi: Super, dziękuję za pomoc

kerajs: Sądzę, iż jest troszeczkę inaczej. ''Z drutu o długości 120 dm wykonano szkielet graniastosłuipa prostego, którego jedna z krawędzi podstawy jest o 6 dm krótsza od drugiej'' czyli: 4x +4( x+6) + 4y = 120 '' Do tego szkieletu przymocowano metalowe płyty, dzięki czemu powstało pudło z górnym wiekiem.'' P(x)= 2*x*y + 2*(x+6)*y + 2*x*(x+6) Koszt drutu jest stały K_d=120*4 zł (nb, ciekawe co to za drut − sztywny i bardzo drogi (40 zł za metr)), wystarczy więc zmaksymalizować koszt płyt K_p(x)=18*P(x) .