Postać iloczyniwa Zofija: Wyznacz pary liczb całkowitych x i y spełniających równanie 3x+xy+y+6=0 Próbowałam to przestawiać, szukać wzorów skróconego mnożenia, ale nie potrafię

Mariusz: x(3+y)+(3+y)+3=0 (x+1)(y+3)=−3 x+1 = −1 ∧y+3 = 3 x+1 = 3 ∧y+3 = −1

Zofija: thx

Saizou : Marusz, trochę za mało przypadków −3 = (−1) * 3 = 1 * (−3) = 3*(−1) = (−3)*1 albo x*(3+y) = −6−y , przy założeniu, że 3+y≠0→y≠−3 (gdyby y = −3, to mamy równanie 3x−3x−3+6=0 sprzeczność)

	6+y		3+y+3		3+y		3		3
x = −		= −(		) = −(		+		) = −(1+		)
	3+y		3+y		3+y		3+y		3+y

	3
Aby x był całkowity, to wyrażenie		musi być całkowite, wówczas
	3+y

3+y musi dzielić 3, stąd 3+y = 1 lub 3+y=−1 lub 3+y=3 lub 3+y=−3 y = −2 lub y = −4 lub y = 0 lub y = −6 x =−4 lub x= 2 lub x =−2 lub x = 0

Mariusz: Saizou nie uwzględniłem jeszcze jednej pary czynników która daje −3 x+1 = −1 ⋀y+3 = 3 x+1 = 3 ⋀ y+3 = −1 x+1 = 1 ⋀ y+3 = −3 x+1 = −3 ⋀ y+3 = 1 Z podejścia które zaproponowałem otrzymalibyśmy cztery rozwiązania (x,y): {(−2,0),(2,−4),(0,−6),(−4,−2)} Saizou nadal za mało ?

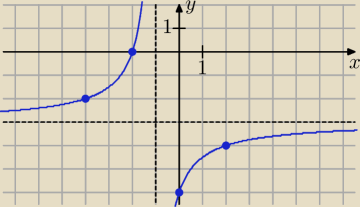
rys: Ilustracja do rozwiązania Mariusza

	−3x − 6		−3
3x+xy+y+6=0 ⇒ y(x + 1) = −6 − 3x ⇒ y =		⇒ y =		− 3
	x + 1		x + 1

syr: