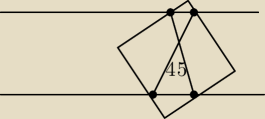
 Dwa kąty kwadratu o boku a wystają poza pas o szerokości a o równoległych krawędziach. Boki
kwadratu przecinają krawędzie paska w czterech punktach. Wykazać, że przekątne czworokąta,
którego wierzchołkami są te punkty, przecinają się pod kątem 45 stopni.
Dwa kąty kwadratu o boku a wystają poza pas o szerokości a o równoległych krawędziach. Boki
kwadratu przecinają krawędzie paska w czterech punktach. Wykazać, że przekątne czworokąta,
którego wierzchołkami są te punkty, przecinają się pod kątem 45 stopni.
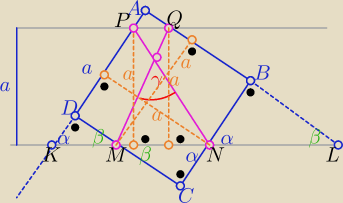 1/ α+β=90o
2/ wystarczy zauważyć,że trójkąty
KNP i MLQ ( mają po dwie wysokości dł. "a") więc są równoramienne
1/ α+β=90o
2/ wystarczy zauważyć,że trójkąty
KNP i MLQ ( mają po dwie wysokości dł. "a") więc są równoramienne
| α | β | |||
zatem |∡NMQ|= 90o− | i |∡MNP|=90o− | |||
| 2 | 2 |
| α+β | ||
to γ= | ||
| 2 |