4 lip 18:26
an:
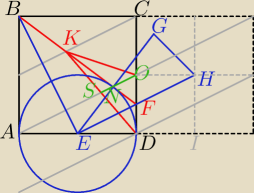
KF oraz OS są środkowymi trójkąta KDO i jako takie przecinają się w jednym
punkcie dzielącym je w stosunku 1:2
NO=2*|NS|=36
7 lip 20:37
www: an a jak doszedłeś do tego ze to środowe, bo zaznaczyłeś punkty G i H w jaki sposób one
powstały
8 lip 11:50
an: trójkąty ENB; ABE; EGH są podobne
8 lip 13:16
an: miało być napisane trójkąty ENB; ABE; EGH są przystające
8 lip 13:39
www: A ten wniosek : KF oraz OS są środkowymi trójkąta− możesz też objaśnić.
8 lip 15:20
Mila:
Jeśli an nie wyjaśni, to napiszę moje wyjaśnienie z lekkim wspomaganiem trygonometrii:
|NF|=|FD| (to wiadomo dlaczego?)
|FD|=|FO| z tryg.
9 lip 16:49
an:
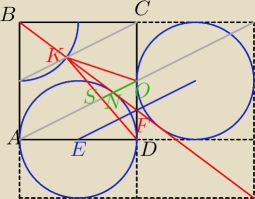
OF=OD wyjaśnia rysunek, natomiast KS=KD po paru "Pitagorasach" dość łatwo w analitycznej ,
przyjmując AB=40 współrzędne punktów są całkowite. Może ktoś poda
rozwiązanie "czysto geometryczne"
9 lip 17:55
Mila:
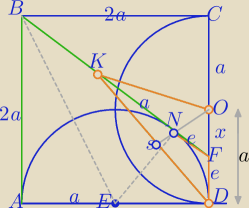
|KN|=a, |SN|=18 cm
1)
W ΔABE:
2)
| | 3 | |
tgβ=tg(90−2α)=ctg(2α)= |
| |
| | 4 | |
W ΔBCF:
| a+x | | 3 | | 1 | | 1 | |
| = |
| ⇔x= |
| a⇒ x=e= |
| a |
| 2a | | 4 | | 2 | | 2 | |
3)
Tw. Menelausa:
ΔKDF przecięty prostą OS:
4) KF, OS− środkowe ΔDKO⇔
|NO|=2*18cm=36cm
9 lip 19:08
10 lip 00:20
Mila:
www zawsze znajdzie coś ciekawego
10 lip 00:44
