dowód geometryczny
Raksi: W trapezie ABCD o podstawach AB i CD przez punkt O przecięcia się przekątnych poprowadzono dwie
proste równoległe do boków BC i AD, Prosta równoległa do boku BC przecina bok AB w punkcie B',
a prosta równoległa do boku AD przecina bok AB w punkcie A'. Wykaż, że |AA'|=|BB'|
3 lip 19:37
Mila:
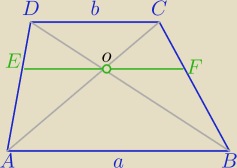
Podpowiedź:
EF||AB
poprowadź równoległe, powstaną równoległoboki.
3 lip 21:18
Raksi: czy jeśli dwa trapezy mają takie same kąty odpowiadające sobie i ramiona odpowiadające sobie
takiej samej długości to możemy stwierdzić, że te trapezy są do siebie takie same, czyli
przystające?
4 lip 21:01
Raksi: skąd wiemy, że |EO|=|OF| ?
4 lip 21:02
4 lip 21:14
Raksi: ciekawe i przydatne zależności. dziękuję.
5 lip 02:04
 Podpowiedź:
EF||AB
Podpowiedź:
EF||AB