Geometria analityczna 06.22
Raksi: (0−6)PR
Dane są okrąg o
1 o równaniu (x−6)
2+(y−4)
2=98 oraz okrąg o
2 o promieniu 2
√5.
Środki okręgów o
! i o
2 leżą po różnych stronach prostej k o równaniu y=−3x−6, a punkty
wspólne obu okręgów leżą na prostej k.
Wyznacz równanie okręgu o
2.
Punkty wspólne o
1 i k
| | 19 | | −87 | |
A(1, −9) B( |
| , |
| ) |
| | 5 | | 5 | |
Równanie okręgu o
2, gdzie S(a,b) to jego środek
(x−a)
2+(y−b)
2=20
Ponieważ A i B należą do okręgu o
2 to możemy je podstawić do jego równania:
(1−a)
2+(9+b)
2=20
z tych dwóch równań otrzymałem (mogą być błędy rachunkowe, lecz nie znalazłem ich)
a=
2314b+42
Następnie postanowiłem spróbować otrzymać dokładne współrzędne z równania
||AS|
2=20
lecz delta wyszła ujemna.
Proszę o dokończenie zadania.
Pozdrawiam
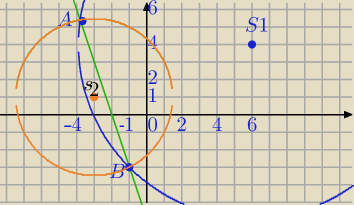o1: (x−6)2+(y−4)2=98
k: y=−3x−6
(x−6)2+(−3x−6−4)2=98