twierdzenie Talesa anonim123: Bok trójkąta podzielono na pięć części w stosunku 1:2:3:4:5 przez punkty podziału poprowadzono proste równoległe do drugiego boku. Wyznacz długość odcinków na jakie podzieliła ta prosta bok trzeci wiedząc że ma on długość 30cm. Wiem że trzeba skorzystać z twierdzenia Talesa

wredulus_pospolitus: no to skoro wiesz że trzeba z Talesa ... to w czym problem

anonim123: narysowałam rysunek i nie wiem co dalej?

anonim123: nie wiem co zrobić, bo mam więcej prostych niż w twierdzeniu

anonim123: Próbowałam tak https://zapodaj.net/5f6a930191377.jpg.html

wredulus_pospolitus:

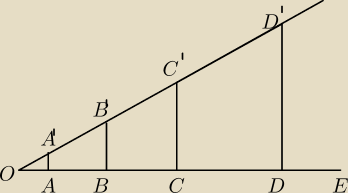
|OA|		|OE|		|OE'|
	=		−−−> |OA| =		= 2
|OA'|		|OE'|		15

|OB|		|OE|		3
	=		−−−> |OB| = |OE'|*		= 6
|OB'|		|OE'|		15

|OC|		|OE|		6
	=		−−−> |OC| = |OE'|*		= 12
|OC'|		|OE'|		15

|OD|		|OE|		10
	=		−−−> |OD| = |OE'|*		= 20
|OD'|		|OE'|		15

Wniosek −−− proporcje z odcinków boku OA będą zachowane dla boku OE' (co powinnaś wiedzieć ze szkoły średniej) Obliczasz |A'B'| , |B'C'| , |C'D'| , |D'E'|

anonim123: A nie można tak jak ja?

anonim123: a odcinek miał być podzielony na 5 części a ty zrobiłeś chyba inaczej

I'm back: Boże kobieto − ostatni odcinek się po prostu nie zmiescil

anonim123: a nie będę potrzebowała odcinka |OE|?

I'm back: Przeanalizuj co napisałem zanim zaczniesz pisać. Jak kontynuowałem to co zrobiłaś.

anonim123: a to co ja zrobiłam jest źle?

anonim123: ale ja już wyliczyłam ten odcinek który był szukany w zadaniu i analogicznie bym chciała wyliczyć inne więc nie rozumiem po co kontynuować

anonim123: czyli jednak mam źle?

wredulus_pospolitus: pomijając fakt, że nie korzystasz z tw. Talesa i robisz bezpodstawne (chociaż słuszne) założenie, to masz dobrze.

anonim123: A to co zrobiłam wcześniej według mnie jest z Talerza wzięłam pod uwagę to zaznaczone na różowo I wydaje mi się że to było to twierdzenie

anonim123: https://zapodaj.net/24799e978e893.jpg.html

wredulus_pospolitus: napisz tw. Talesa Zamieść od razu rysunek wraz z oznaczeniami

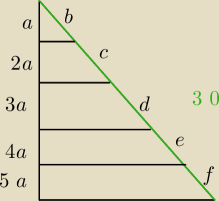
wredulus_pospolitus: b+c+d+e+f = 30 z tw. Talesa:

b		30
	=
a		a+2a+3a+4a+5a

b+c		30
	=
a+2a		a+2a+3a+4a+5a

b+c+d		30
	=
a+2a+3a		a+2a+3a+4a+5a

b+c+d+e		30
	=
a+2a+3a+4a		a+2a+3a+4a+5a

anonim123: A takie zadanie Ramię trapezu podzielono na trzy części w stosunku 1:3:4 licząc od krótszej podstawy Przez punkty podziału poprowadzono proste równoległe do podstaw. Oblicz długości odcinków prostych równoległych zawartych między ramionami trapezu jeżeli wiadomo że długości podstaw trapezu wynoszą odpowiednio 50cm i 30cm nie widzę tu twierdzenia Talesa

anonim123: ?

Eta:

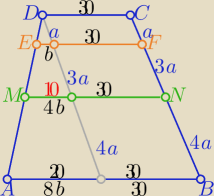
	30+50
|MN|=		=40 −− dł. środkowej trapezu ABCD
	2

|AB|=8b+30=50 ⇒ b=2,5 |EF|=b+30=......... |MN|= 4b+30 = 40

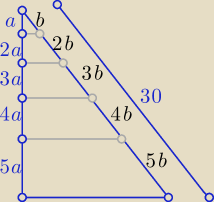
Eta: 15b=30 cm ⇒ b=2 cm i masz dł. poszczegónych odcinków : 2 cm,4 cm,6 cm,8 cm,10 cm i po ptokach

anonim123: A to z 15:49 jest z twierdzenia Talesa? Dlaczego |AB|=8b+30?

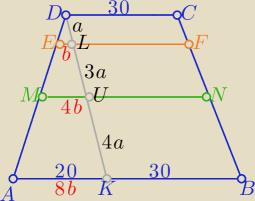
Eta: bo ΔAKD podobny do ΔDEL w skali k= 8 to 8b=20 ⇒ b=2,5 dlatego |AB|= 8b+30 =50 ⇒ 8b=20 i Δ MUD podobny do Δ DEL w skali k=4 to |MU|=4b =10

anonim123: A mogę prosić o rozwiązanie twierdzeniem Talesa, bo teraz to przerabiamy?

Eta: Z tw. Talesa

	|AK|		|DK|		8a
		=		=		= 8
	|EL|		|DL|		a

to |AK|=8|EL| i |EL|=b |AK|=8b=20 cm to |EL|= 20/8=2,5 =b to |AK| = 20=8b

anonim123: nie mogę znaleść wzoru z którego korzystałaś w 17:49 tego z twierdzenia Talesa?

anonim123: Dziękuję