Rachunek Prawdopodbieństwa - Kombinacje
Podstawowy Luigy: Hej, mam takie zadanko z listy wakacyjnej z korków.
Naszkicuj wykres funkcji rozkładu prawdopodobieństwa P(n) dla wystąpienia sukcesu czyli
wystąpienia zdarzenia pozytywnego (bez zdarzeń negatywnych).
Do wyprowadzenia zależności należy zastosować kombinacje czyli wzór Newtona.
(Nwm jak go użyć. Chyba że chodzi o wyprowadzenia wzorów skróconego mnożenia).
Dziedzina funkcji to n ∊ [0;10] ⋀ n ∊ Z, gdzie n to ilość zdarzeń negatywnych
występujących w danej sytuacji.
W zadaniu wykaż się sprytem i nie licz żmudnie wszystkich 10 prawdopodobieństw.
Znajdź relację między nimi. Nadto podaj wzór tej funkcji i nazwę tej funkcji.
Oraz wyznacz na logikę ograniczenie funkcji gdy n → +∞.
Podsumowując:
a.) Wykres P(n) dla n ∊ [0;10] ⋀ n ∊ Z
b.) Wzór i nazwa funkcji
c.) limn → +∞ P(n)
1 lip 17:14
wredulus_pospolitus:
prawdopodobieństwo sukcesu i porażki jest jednakowe i równe 0.5

1 lip 17:20
Podstawowy Luigy: ale dla np. 7 zdarzeń negatywnych już nie raczej. Nic mi to nie mówi.
A ja mam to prawdopodobieństwo obliczyć na kombinacja że P = |A|/|Ω|
1 lip 17:31
wredulus_pospolitus:
nie odpowiedziałeś mi na pytanie
1 lip 17:36
wredulus_pospolitus:
aaa już kumam o co chodzi
.....
zauważ, że:
P(0) = P(10) ;
P(1) = P(9) ;
P(2) = P(8) ;
P(3) = P(7) ;
P(4) = P(6)
1 lip 17:39
Podstawowy Luigy: z tym 0.5 tak masz racje nie zauważyłem znaku zapytania emotykonowego
1 lip 18:02
Podstawowy Luigy: Troche to co napisałeś wyżej to skomplikowane jest.
| | | |
Wydaje mi się że |A| = 1 zawsze tutaj czyli równe | |
| | |
Ω po twoim uproszczeniu na koniec w sumie sprowadza się do np.
1 lip 18:07
1 lip 18:15
wredulus_pospolitus:
Nie mam bladego pojęcia o czym Ty piszesz
1 lip 18:22
Podstawowy Luigy: Pytam czy pokazałem poprawne rozwiazanie
1 lip 18:30
wredulus_pospolitus:
ja kompletnie nie rozumiem co masz pokazać w zadaniu ... dobra ... tym jest P(3)

co to
oznacza?
1 lip 18:36
Podstawowy Luigy: Ten wykres to odpowiedź to A.) wzór i nazwa do B.) Granica do C.)
Wykres wygenerowałem zauważywszy że P(0) = 1, P(1)=50% P(2) = 25% , P(n)=1/|Ωn|
1 lip 18:42
wredulus_pospolitus:
CZYM JEST P(3)

1 lip 18:51
wredulus_pospolitus:
czym jest Ω
n 
1 lip 18:51
Min. Edukacji: Za korki się płaci 😃
1 lip 19:16
Podstawowy Luigy: Ωn − to przestrzeń naszych zdarzeń wszystkich zdarzeń.
Załóżmy że mamy plagi egipskie o konkretnej nazwie od X1 do x7.
I mamy na przykład przypadek: brak plag czyli sukces lub 7 przypadków jednej osobnej plagi lub
Wystąpienie plagi x1 x4 x8 na raz etc.
P(n) to prawdopodobieństwo sukcesu. i jeżeli mamy do
czynienia gdzie może wystąpić tylko 3 plagi to
Probability sukcesu to 12,5% , 7 plag to (1/2)7 *100%
2 lip 12:34
wredulus_pospolitus:
"jeżeli mamy do
czynienia gdzie może wystąpić tylko 3 plagi to
Probability sukcesu to 12,5%"
Probability czego?
No dobra i ponownie się pytam CZYM JEST P(3)

Prawdopodobieństwem osiągnięcia ilu sukcesów w ilu próbach

2 lip 14:24

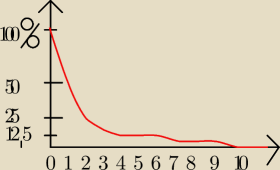 P(N) = (1/2)n
P(N) = (1/2)n 
 hiperboliczna funkcja
hiperboliczna funkcja 
 Ograniczenie Dolne limes n→+∞ = 0
Ograniczenie Dolne limes n→+∞ = 0 

 co to
oznacza?
co to
oznacza?


 Prawdopodobieństwem osiągnięcia ilu sukcesów w ilu próbach
Prawdopodobieństwem osiągnięcia ilu sukcesów w ilu próbach 