kula w metryce
szarik:
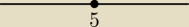
Narysować kulę w odległości dyskretnej na R
K(5,1)
kula w metryce dyskretnej w przypadku gdy r∊(0,1] to jest {x}. Czyli w tym wypadku (x=5, r=1)
to będzie po prostu jeden punkt na prostej? Nie chce mi się wierzyć, że to takie proste
30 cze 22:46
szarik: up
1 lip 15:36
ite:
tak, ta kula (otwarta) w metryce dyskretnej jest zbiorem składającym się z jednego punktu
K(5,1) = {5}
p.s. szarik znaczy kulka
2 lip 16:36
szarik: czyli jednak takie proste

dzięki
ite. jeszcze jedno pytanie.
muszę wykazać nierówność trójkąta dla metryki rzeki. Nie mogę sobie poradzić z przypadkiem gdy
x
1≠y
1.
wtedy d(x,y)=|x
1−y
1|+|x
2|+|y
2|. Jak wykazać, że d(x,y)≤d(x,z)+d(z,y)?
Nie chodzi mi o całe rozwiązanie. Chcę to zrobić sama, tylko z jakiej własności skorzystać, od
czego zacząć?
5 lip 16:33
ite:
Przypadek gdy x1≠y1 proponuję rozbić na dwa główne przypadki:
1/ z1=x1 lub z1=y1 (punkt z leży na tej samej prostej prostopadłej do rzeki co jeden z
punktów x lub y)
2/ z1≠x1 i z1≠y1 (punkt z leży na innej prostej prostopadłej do rzeki niż którykolwiek z
punktów) i tu chyba nie da się ominąć dwóch podpunktów
6 lip 14:08
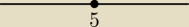 Narysować kulę w odległości dyskretnej na R
K(5,1)
kula w metryce dyskretnej w przypadku gdy r∊(0,1] to jest {x}. Czyli w tym wypadku (x=5, r=1)
to będzie po prostu jeden punkt na prostej? Nie chce mi się wierzyć, że to takie proste
Narysować kulę w odległości dyskretnej na R
K(5,1)
kula w metryce dyskretnej w przypadku gdy r∊(0,1] to jest {x}. Czyli w tym wypadku (x=5, r=1)
to będzie po prostu jeden punkt na prostej? Nie chce mi się wierzyć, że to takie proste
 dzięki ite. jeszcze jedno pytanie.
muszę wykazać nierówność trójkąta dla metryki rzeki. Nie mogę sobie poradzić z przypadkiem gdy
x1≠y1.
wtedy d(x,y)=|x1−y1|+|x2|+|y2|. Jak wykazać, że d(x,y)≤d(x,z)+d(z,y)?
Nie chodzi mi o całe rozwiązanie. Chcę to zrobić sama, tylko z jakiej własności skorzystać, od
czego zacząć?
dzięki ite. jeszcze jedno pytanie.
muszę wykazać nierówność trójkąta dla metryki rzeki. Nie mogę sobie poradzić z przypadkiem gdy
x1≠y1.
wtedy d(x,y)=|x1−y1|+|x2|+|y2|. Jak wykazać, że d(x,y)≤d(x,z)+d(z,y)?
Nie chodzi mi o całe rozwiązanie. Chcę to zrobić sama, tylko z jakiej własności skorzystać, od
czego zacząć?