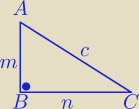
praw-stwo Ala: Dwie różnie liczy naturalne m i n zostały wylosowane z zakresu [1, 72] tak, że m < n. Niech ABC będzie trójkątem prostokątnym o kącie prostym w B, AB = m i BC = n. Jakie jest prawdopodobieństwo, że AC² jest podzielne przez 73?

kerajs:

	1
|AC|=73=32+82 ⇒ m=48 i n=55 ⇒ P=
	72*71

Szkolniak: A jeśli, przykładowo, m=5 i n=11? Ten zestaw nie pasuje? Ja to próbowałem rozwiązać, ale doszedłem do tego że trzeba rozwiązać równanie: m²+n²=73k, gdzie k∊{1,2,3,...,140}, n,m∊ℕ oraz m<n No i wszystkich możliwości, tzn. |Ω|=36*71.

Mila: c²=m²+n² 73|c² c²=k*73 Dla liczb pierwszych k postaci k=4n+1 mamy : 1) k=5 c²=5*73 Z tożsamości Fibonacciego: 5*73=(1²+2²)*(3²+8²)=(1*3+2*8)²+(1*8−2*3)²=19²+2² m=2, n=19 lub 5*73=(1*3−2*8)²+(1*8+2*3)²=13²+14² m=13, n=14 2) k=13 c²=13*73 mamy: m=7, n=30 lub m=18, n=25 czyli po dwa przypadki dla każdej k=4n+1 ( liczby pierwszej) 3) to ustal jak będzie możliwa największa liczba k , w pozostałych przypadkach jeszcze nie wiem. Znalazłeś parę dla innych k ?

Mila: dla k=73 jeden rozkład, jak podał kerajs.

Szkolniak: Ja próbowałem coś z twierdzeń na temat liczb pierwszych, szukanie parzystości i nieparzystości sum dwóch liczb podniesionych do kwadratu, ale strasznie dużo tego rozpatrywania różnorodnych opcji.. Według tego co mówisz Mila, to w Twoim przypadku największą liczbą 'k' będzie 137? I trzeba zliczyć ile jest tych liczb w przedziale [1;140] i pomnożyć razy dwa?

Mila: k=137 już nie może być, bo 137*73=65²+76² albo 137*73=1²+100²

Szkolniak: Nad tym nie pomyślałem, bo w sumie nie wiedziałem nawet co to dokładnie jest ta Tożsamość Fibonacciego (Brahmagupty). Ale zaraz spróbuję pomyśleć nad ograniczeniem tutaj odnośnie 'k'. Swoją drogą, czy dobrze wyliczyłem ile jest wszystkich możliwych przypadków tutaj? Tzn. 36*71.

Mila: Przedstawianie liczby naturalnej jako sumy kwadratów dwóch liczb naturalnych. Podróże po imperium liczb. Andrzej Nowicki. Było w pdf. poszukaj.

kerajs: Przepraszam, za błędną odpowiedź. Jakoś mi się wydawało, że i przeciwprostokątna ma być liczbą naturalną, a stąd jedyna wskazana powyżej możliwość. Jak teraz widzę, w treści zadania nie ma takiego ograniczenia.

Ala: Czy największe k będzie 125?