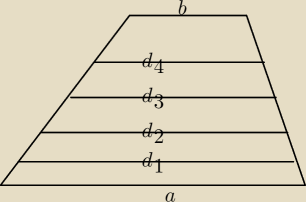
Trapez o podstawach a>b
podzielono odcinkami równolegymi do podstaw, na 5 trapezów o równych polach
Wykaż, że suma kwadratów długości tych odcinków
jest równa podwojonej sumie kwadratów długości podstaw
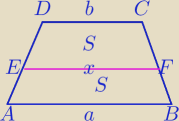Podpowiedź:
AB II DC
1)
Średnia kwadratowa w trapezie.
W dowolnym trapezie długość odcinka równoległego do podstaw trapezu i dzielącego trapez
na dwa trapezy o równych powierzchniach jest równa średniej kwadratowej.
x=√a2+b22⇔
| a2+b2 | ||
x2= | ||
| 2 |
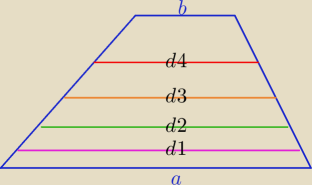Można wyprowadzić, korzystając z podpowiedzi poprzedniczki 
taki wzorek
dk=√((n−k)a2+kb2)/n
gdzie : n −− ilość trapezów z podziału , k −− k−aty odcinek licząc od podstawy "a"
i mamy:
| 4a2+b2 | ||
d12= | ||
| 5 |
| 3a2+2b2 | ||
d22= | ||
| 5 |
| 2a2+3b2 | ||
d32= | ||
| 5 |
| a2+4b2 | ||
d42= | ||
| 5 |