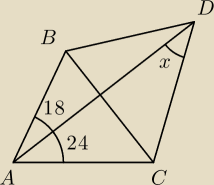
katy mikus: Wiadomo że AB = BC i AC = BD oblicz miarę kąta x.

chichi: Coś dobuduj i miara kąta się sama ukaże

mikus: A co dobudować?

Mariusz: Z równości AB = BC wynika że trójkąt ABC jest równoramienny zatem kąty przy podstawie mają równe miary Mamy także daną miarę kąta przy podstawie więc z sumy miar kątów w trójkącie dostaniemy miary wszystkich kątów w trójkącie ABC Miary kątów trójkąta ABC to 42 , 42, 96 Z sumy miar kątów w trójkącie ACD dostajemy 24+42+y+x = 180 66+x+y = 180 x+y = 114 Trójkąty ABC oraz BCD mają dwa boki równej długości (BC wspólny a równość długości drugiej pary boków jest dana treścią zadania) jednak jest to za mało aby stwierdzić że trójkąty ABC oraz BCD są przystające

chichi: No bo nie są...

Mariusz: Jak na razie wykorzystana została równość długości boków AB=BC i zadanie wyznaczenia miary kąta ADC zostało sprowadzone do wyznaczenia miary kąta BCD Trzeba by jakoś wykorzystać równość długości boków AC = BD

Mariusz: Można dokończyć z twierdzenia sinusów i cosinusów Z twierdzenia sinusów w trójkącie ABC

AC		BC
	=
sin(96)		sin(42)

AC		BC
	=
sin(84)		sin(42)

AC		BC
	=
2sin(42)cos(42)		sin(42)

	2sin(42)cos(42)
AC =		BC
	sin(42)

AC = 2cos(42)BC BD = 2cos(42)BC

	BD
BC =
	2cos(42)

Z twierdzenia sinusów w trójkącie ACD

AC		CD
	=
sin(x)		sin(24)

	sin(24)
CD =		AC
	sin(x)

	sin(24)
CD =		BD
	sin(x)

Z twierdzenia cosinusów w trójkącie BDC

	BD2		sin2(24)
BD2=		+		BD2−
	4cos2(42)		sin2(x)

	sin(24)		BD
2		BD		cos(114−x)
	sin(x)		2cos(42)

	1		sin2(24)		sin(24)
BD2=BD2(		+		−		cos(114−x))
	cos2(42)		sin2(x)		sin(x)cos(42)

	1		sin2(24)		sin(24)
1 =		+		−		cos(114−x)
	cos2(42)		sin2(x)		sin(x)cos(42)

No i mamy równanie trygonometryczne

Mariusz: Tutaj mała pomyłka

	1		sin2(24)		sin(24)
1 =		+		−		cos(114−x)
	4cos2(42)		sin2(x)		sin(x)cos(42)

To równanie trygonometryczne sprowadza się do równania kwadratowego na ctg(x) Jedno rozwiązanie tego równania trzeba odrzucić i zostaje ctg(x) = √3 a z tego wynika że x = 30

mikus: Dzieki Mariusz a da się rozwiązać właśnie coś dorysowując niż trygonometrią?

Mariusz: To pomysł chichiego więc może on coś podrzuci ale gdybyśmy dorysowali trójkąt równoboczny O boku CD i zdołali zauważyć że BD jest prostopadły do boku dorysowanego trójkąta to byśmy mieli to co chcą w zadaniu

Mariusz: Prostopadły ma być bok AC do boku dorysowanego trójkąta równobocznego o boku CD ale to jest tylko kombinowanie na podstawie znajomości wyniku

Mariusz: Dałoby się jakoś pokazać że AD jest prostopadły do jednego z boków dorysowanego trójkąta równobocznego o boku CD ?

chichi: @Mariusz podał prawidlowy wynik, który wymagał nieco pracy. pokaże syntetyczne rozwiązanie jak tylko znajdę czas, ale na tym forum są jeszcze zaawansowani geometrzy, więc może pojawi się coś wcześniej

Mariusz: Nie mam pomysłu co dobudować Gdybyśmy dobudowali trójkąt równoboczny to trzeba by było pokazać że otrzymaliśmy kąt prosty a gdybyśmy dobudowali trójkąt prostokątny to trzeba by było pokazać odpowiedni stosunek długości boków Gdybyśmy chcieli rozpisać trochę to równanie trygonometryczne to otrzymamy

1		sin2(24)		sin(24)	cos(66+x)
	− 1 +		+			=0
4cos2(42)		sin2(x)		cos(42)	sin(x)

1		sin2(24)
	− 1 +
4cos2(42)		sin2(x)

	sin(24)	cos(66)cos(x)−sin(66)sin(x)
+			=0
	cos(42)	sin(x)

1		sin2(24)
	− 1 +
4cos2(42)		sin2(x)

	sin(24)cos(66)	cos(x)		sin(66)sin(24)
+			−		=0
	cos(42)	sin(x)		cos(42)

1		cos2(x)+sin2(x)
	− 1 + sin2(24)(		)+
4cos2(42)		sin2(x)

sin2(24)	cos(x)		sin(24)cos(24)
		−		=0
cos(42)	sin(x)		cos(42)

1
	− 1 +
4cos2(42)

	cos2(x)		sin2(24)	cos(x)
sin2(24)(		+1)+
	sin2(x)		cos(42)	sin(x)

	sin(48)
−		=0
	2cos(42)

1		sin2(24)		cos(42)
	− 1 + sin2(24)(ctg2(x)+1)+		ctg(x)−		=0
4cos2(42)		cos(42)		2cos(42)

1		sin2(24)
	− 1 + sin2(24)ctg2(x)+sin2(24) +		ctg(x)
4cos2(42)		cos(42)

	cos(42)
−		=0
	2cos(42)

1		sin2(24)
	−cos2(24)+ sin2(24)ctg2(x)+		ctg(x)
4cos2(42)		cos(42)

	cos(42)
−		=0
	2cos(42)

sin²(24)ctg²(x)+

	sin2(24)		1−4cos2(42)cos2(24)−2cos2(42)
		ctg(x)+		=0
	cos(42)		4cos2(42)

	1		1−4cos2(42)cos2(24)−2cos2(42)
ctg2(x)+		ctg(x)+		=0
	cos(42)		4cos2(42)sin2(24)

t=ctg(x)

	1		1−4cos2(42)cos2(24)−2cos2(42)
t2+		t+		=0
	cos(42)		4cos2(42)sin2(24)

	1		1−4cos2(42)cos2(24)−2cos2(42)
(t+		)2+
	2cos(42)		4cos2(42)sin2(24)

	1
−		= 0
	4cos2(42)

	1		1−sin2(24)−4cos2(42)cos2(24)−2cos2(42)
(t+		)2+		=0
	2cos(42)		4cos2(42)sin2(24)

	1		cos2(24)−4cos2(42)cos2(24)−2cos2(42)
(t+		)2+		=0
	2cos(42)		4cos2(42)sin2(24)

	1		4cos2(42)cos2(24)+2cos2(42) − cos2(24)
(t+		)2−		=0
	2cos(42)		4cos2(42)sin2(24)

	−sin(24)−√4cos2(42)cos2(24)+2cos2(42) − cos2(24)
t1 =
	2cos(42)sin(24)

	−sin(24)+√4cos2(42)cos2(24)+2cos2(42) − cos2(24)
t2 =
	2cos(42)sin(24)

Tutaj przydałoby się dalej uprościć to rozwiązanie Rozwiązanie t₁ należy odrzucić bo otrzymany kąt miałby zbyt dużą miarę Rozwiązanie syntetyczne na pewno będzie szybsze Na rozwiązanie z użyciem trygonometrii łatwiej wpaść bo tego w szkole uczą

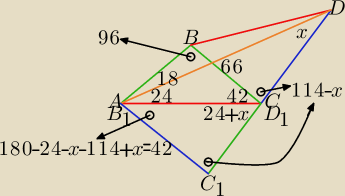
Koszałek Opałek: Proponuję takie rozwiązanie. Równą długość mają odcinki zielone oraz czerwone, liczby to miary kątów w stopniach. Linia C₁ − C (D₁) − D jest prosta. Pokrywają się punkty A i B₁ oraz C i D₁. Trójkąt BCD został przesunięty do B₁C₁D₁, odcinki AC i B₁D₁ pokrywają się. |∡C₁B₁D₁| = |∡ACB| = 42 (kąty naprzemianległe), zatem czworokąt AC₁CB jest trapezem i AC₁ ∥ BC, stąd |∡C₁AB = 42 + 24 + 18 = 84 = |∡AC₁C| = 114 − x ⇒ x = 114 − 84 = 30 albo 96 = |∡ABC| = |∡BCC₁| = 42 + 24 + x ⇒ x = 30

chichi: @Mariusz ja wiem, że to najprościej wpaść na takie z użyciem trygonometrii, aczkolwiek równania, które otrzymujesz są wg mnie też trudne do rozwiązania dla licealistów

mikus: |∡C1B1D1| = |∡ACB| czemu one naprzemianległe?

Mariusz: Niech E będzie przecięciem boków AD i BC chichi no ja gdy próbowałem bez trygonometrii to doszedłem tylko do tego że ABC jest równoramienny skąd przy danej mierze jednego kąta wyznaczyłem wszystkie kąty trójkąta ABC korzystając z tego że suma miar kątów jest równa 180 Następnie z sumy miar kątów w trójkącie ACD uzależniłem miary kątów w trójkącie CDE od x I gdyby nie pomysł z trygonometrią to nie wiedziałbym jak dalej dokończyć

	−sin(24)+√4cos2(42)cos2(24)+2cos2(42)−cos2(24)
t2=
	2sin(24)cos(42)

Tutaj można by spróbować licznik doprowadzić do wzoru na cosinusa sumy bądź różnicy a mianownik można by spróbować doprowadzić do wzoru na sinusa sumy bądź różnicy Ponieważ miara kątów jest podzielna przez 3 więc można by też spróbować wyrazić wartości funkcji trygonometrycznych tych kątów za pomocą pierwiastków i dalej bawić się upraszczaniem Gdybyśmy chcieli skorzystać z pierwszej propozycji to w t₁ mamy w liczniku różnicę a więc należałoby dążyć do cosinusa różnicy W t₂ natomiast w liczniku mamy sumę a więc należy dążyć do cosinusa różnicy Po podejrzeniu wyników dla t₁ oraz t₂ w programie komputerowym wnioskuję że należy dążyć do

	cos(96+66)
t1=
	sin(96+66)

	cos(96−66)
t2=
	sin(96−66)

Tutaj widzimy że t₁ daje kąt o zbyt dużej mierze

mikus: Ponawiam czemu |∡C1B1D1| = |∡ACB| są naprzemianległe?

mikus: Jak ten trójkąt BCD został przesunięty?

mikus: Nie wiem nadal czemu tam są kąty naprzemianległe

www: https://math.stackexchange.com/questions/4478459/find-angle-x-in-the-figure-below

www.sierotka: hej www i po co to pokazujesz?, co chciałeś powiedzieć?