Zadanie na wymiary trapezu i prostokąta w składzie większej figury profjan: Jest figura ABFGCD, która jest złożeniem prostokąta ABFE, trapezu EFGH i prostokąta HGCD. Nie potrafię zamieścić rysunku, więc opiszę jak najdokładniej, nawet jeśli coś jest powtórzeniem lub oczywistością. Dane: (tylko trzy miary) bok AB = k; bok AD = h, bok AE (część boku AD) = m; Dane: czyli AB = k = EF Dane: znana jest powierzchnia P figury ABFGCD. Dane: można wyliczyć powierzchnię prostokąta ABFE, bo jest znane AB i AE, czyli k*m Warunek: bok AD = bok AE + bok EH + bok HD (czyli h = m + n + p). Warunek: Pole ABFE = Pole EFGH = Pole HGCD = 1/3 Pola ABFGCD. Warunek: z poprzedniego wynika: k*m = x*p = n*((k+x)/2) Warunek: AB = k = EF oraz HG = x = CD. Warunek: równoległe są: GC, BF, AD, czyli też AE, DH, HD. Warunek: x > k Szukane: wzór na x Szukane: wzór na n Szukane: wzór na p Innymi słowy szukamy wymiarów środkowego trapezu oraz górnego prostokąta. Dziękuję.

profjan: Droga Milu, prawie o to mi chodziło. Bo chodziło mi o to, żeby to ten górny HGCD był "chudszy i dłuższy", czyli żeby x > k. Usiłowałem to ukazać w ostatnim warunku z zadania. wtedy też p < m. wtedy też bok FG w trapezie jest pod odwrotnym kątem. dziękuję

Mila: Dobrze poprawiam Nie uwzględniłam warunku x>k.

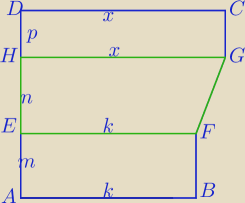
Mila: ABFE,trapezu EFGH i prostokąta HGCD. x>k, p<m 1) [ ABFGCD]=3S

profjan: Droga Milu, dziękuję. Właśnie tak to widziałem. Wydaje mi się też, co do ścisłości, że będzie tak: m > n > p. I mam nadzieję, że Ty lub Wredulus, to rozwiążecie i będę miał piękny wzór na n, p i x. dziękuję.

Mila: To już jutro, tymczasem Dobranoc