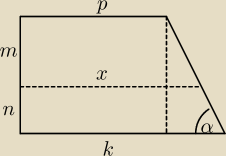
podział trapezu prostokątnego na dwie równe figury profjan: Jest trapez prostokątny ABDC o bokach równoległych k (odcinek AB) i p (odc. CD). Znany jest też bok stanowiący wysokość h (odc. AC). Zostaje przeprowadzony odcinek x (odc. EF) równoległy do boków k i p, który dzieli ten trapez na dwie figury o równych powierzchniach. Dana jest jeszcze długość odcinka m (odc. CE). Czyli m+n = h. Pytanie 1. Ile wynosi odcinek x wyrażony wzorem z danych k, p, h i m? Pytanie 2. Ile wynosi odcinek n (odc. EA) wyrażony wzorem z danych k, p, h i m?

wredulus_pospolitus: chyba coś nie tak z oznaczeniami ... jak AC może być bokiem trapezu ABCD Jak już to AD

wredulus_pospolitus: AB = k EF = x CD = p wiemy, że:

k+x		p+x		pm−kn
	*n =		*m −−−> x(n−m) = pm − kn −−> x =
2		2		n−m

wredulus_pospolitus: pytanie 2 jest bez sensu: n = h−m koooniec

profjan: Dziękuję Wredulusowi Pospolitusowi, ale zauważyłem, że w tekście zadania jest źle przeze mnie napisane. Dane jest tylko k, p i h. I oczywiście h= AD, błąd wynikał z pośpiechu. Szukane jest x oraz m i n (jakkolwiek m+n = h, więc jedno z nich wystarczy). Chciałbym dołączyć fotografię z rysunkiem, ale nie potrafię. Dane: h, p i k. Warunek: pole EFCD = pole ABFE Szukane: x oraz m (lub n). Dlatego pytanie powinno brzmieć: Pytanie 1. Ile wynosi x wyrażone przez k, p i h. Chodzi o formułę x = wzór Pytanie 2. Ile wynosi m wyrażone przez k, p i h (alternatywnie: ile wynosi n wyrażone przez k i h). Dziękuję.

wredulus_pospolitus: musimy kombinować 'podobnie' do tego co w drugim zadaniu

	k−p		x−p		x−p
ctgα =		=		−> m =		*h
	h		m		k−p

x+p		k+p		x−p
	*m = 0.5		*h −−−> (x+p)*		*h = 0.5U(k+p)*h −−−>
2		2		k−p

	k2+p2		√2(k2+p2)
−−−> x2−p2 = 0.5 (k2−p2) −−−> x2 =		−−−> x =
	2		2

a stąd mamy:

	.... − p
m =		*h
	k−p

Mila: Cześć Arturze. Bardzo jestem zadowolona z Nortona. Zainstalowany. Komputer chyba szybciej działa Dziękuję . Pozdrawiam.

profjan: Do Wredulusa Pospolitusa: dziękuję za rozwiązanie. To mi bardzo pomogło. ten x jest bardzo ładny. Czy można m (albo n) wyrazić jakimś "ładnym" "prostszym" wzorem? Do Mili: czy to jest komentarz do mnie, czy do Wredulusa? pozdrowienia ProfJan

Mila: Do Wredulusa , to komentarz do wcześniejszej wymiany opinii n.t. antywirusa. Dziękuję za pozdrowienia Panie ProfJanie Też pozdrawiam. POwodzenia w zmaganiach z królową nauk.