opisz zbiór nervous: Opisz zbiór Z x R ∪ R x R jako podzbiór R²

Maciess: To może prościej. Jak mamy zbiór {1,2,3} i dodamy go do zbioru wszystkich liczb naturalnych to jaki zbiór otrzymamy?

nervous: otrzymamy zbiór liczb naturalnych? w poleceniu jest jednak Z x R U R x Z

Maciess: No dokładnie. Ale w poleceniu jest coś innego niż napisałeś o 23:02. Jaka w koncu jest oryginalna treść?

Maciess: Jesli tresc jest jak w 23:02 to narysuj na płaszczyźnie zbiór {1}xR, {2}xR, {0}xR itd. Co otrzymujesz?

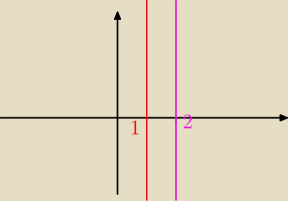
nervous: Dobrze narysowane? Czyli zbiór liczb R?

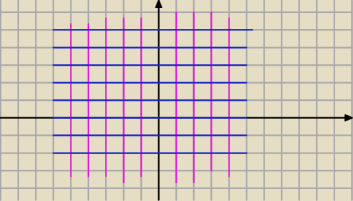
Maciess: To nie jest zbiór R (choć w pewnych sytuacjach można by to było utożsamić). To jest podzbiór R². No i widzisz ze wychodzą proste pionowe. Czyli ZxR to będą takie proste pionowe, przechodzące punkty całkowite. Analogicznie ten drugi zbiór to będą proste poziome. Jak nalozysz na siebie proste pionowe i poziome to otrzymasz taką kratę. Teraz ten opis. Ma być słowny czy mamy to zapisać w postaci {x: P(x)}?

nervous: Nie jest podane, po prostu chciałabym zrozumieć o co dokładnie chodzi, więc najlepiej oba : )

Maciess: No to słownie to mamy kratkę na płaszczyźnie i rysunek wystarczy. Mozna tez ten zbiór zdefiniowac tak: Zbiór punktów na płaszczyźnie, takich że przynajmniej jedna współrzędna jest całkowita. {(x,y)∊R²: x∊Z v y∊Z}

nervous: Dziękuję bardzo!