Jednokładności anonim: Niech O1 = O((−2, −1), 1) i O2 = O(S2, 2), gdzie S2 = (8, 4). Wyznaczyć wszystkie jednokładności przekształcające okrąg O1 na O2

kerajs: Stosunek promieni wyznacza skalę jednokładności: |k|=r₂/r₁ a stąd dla k=2 środkiem jednokładności jest (−12,−6) , a dla k=−2 środkiem jednokładności jest (4/3,2/3)

123: czyli rozumiem, ze s1s2=(10,5). skad w takim razie otrzymalimy srodek jednokładności (4/3, 2/3)? z obliczen rozumiem że tam powinno być 1/3 * s1s2 = 1/3 * (10,5) = (4/3, 2/3) − tylko własnie skąd wiemy że musimy pomnożyć przez 1/3?

kerajs: ''123: czyli rozumiem, ze s1s2=(10,5).'' W Polsce współrzędne wektorów piszemy w nawiasach kwadratowych. Niestety, tutejszy edytor jest bardzo prymitywny, ale i w nim można próbować poprawniej to zapisać: S₁^→S₂=[10;5] ''123: (...) rozumiem że tam powinno być 1/3 * s1s2 = 1/3 * (10,5) = (4/3, 2/3) '' Druga równość tu nie zachodzi! Przyznaję, środki jednokładności wskazałem z głowy (z podobieństwa trójkątów), ale na maturze pisałbym coś takiego: Niech P będzie środkiem jednokładności o skali k=−2, a wtedy: P^→S₂=−2*P^→S₁ Skoro S₁^→S₂=S₁^→P + P^→S₂ to S₁^→S₂=S₁^→P − 2* P^→S₁ więc S₁^→S₂=3*S₁^→P [10,5]=3[x_P−(−2); y_P−(−1)] co daje układ: 10=3x_P+6 ∧ 5=3y_P+2 którego rozwiązaniem jest punkt który wskazałem. A 1/3 o którą pytasz masz tu [10,5]=3[x_P−(−2); y_P−(−1)]

1
	[10,5]=[xP−(−2); yP−(−1)]
3

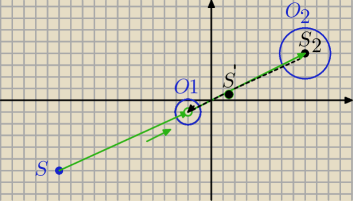
Mila: |k|=2 1) k=2 S₁=(−2,−1), S₂=(8,4) S=(a,b) − środek jednokładności Dodaję rysunek: (8,4)=J²_S( (−2,−1) ) SS₂^→=2*SS₁^→ [8−a,4−b]=2*[−2−a,−1−b]⇔[8−a,4−b]=[−4−2a,−2−2b] 8−a=−4−2a, 4−b=−2−2b a=−12, b=−6 S=(−12,−6) 2) k=−2 S'S₂^→=(−2)*S'S₁^→ [8−a,4−b]=(−2)*[−2−a,−1−b] [8−a,4−b]=[4+2a,2+2b] 8−a=4+2a i 4−b=2+2b 3a=4 i 3b=2

	4		2
a=		i b=
	3		3

	4		2
S'=(		,		)
	3		3