moneta probability:

	1
Jaką grubość powinna mieć moneta, aby prawdopodobieństwo upadnięcia na kant wynosiło		?
	4

wredulus_pospolitus: A skąd to pytanie? Bo nie podejrzewam oto, że takie zadanie dał nauczyciel.

probability: owszem nauczyciel od rachunku prawdopodobieństwa

probability:

	1
p =		sry
	3

kerajs: Czym są s, r i y?

I'm back: Keraj.. To raczej było 'sorry' skrócone do sry

I'm back: Wtedy dobrze ze sry a nie sra

.: s=sciszony r=rechot y=yeti or s=sample r=random (for) y=yahoo

kerajs: Zajarzyłem. Zamiast p=1/4 ma być 1/3. A to sporo zmienia, gdyż wtedy moneta może być dowolnej szerokości bo są trzy możliwości jej upadku: awers, kant i rewers. A serio, to mam wrażenie, iż przy walcu wpływ na wynik będzie miał sposób rzucania.

ite: Gdyby sposób rzucania można nie miał znaczenia, to dla dla szukanego p=1/3 grubość monety powinna być połową jej promienia.

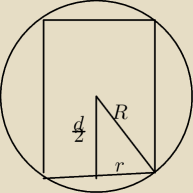
daras: To zadanie John von Neumann rozwiązał w 15 s Moneta stanie na kancie (nie przewróci się), gdy wektor siły ciężkości monety przechodzi przez podstawę.

	2
d =		R
	3

	d
tw. Pitagorasa: (		)2 +r2 =R2
	2

	2√2
r=		R
	3

	r
czyli		=√2
	d

daras: A to czy wypadnie orzeł czy reszka czy też moneta upadnie na kant zależy nie tyle od sposobu rzucania, co podłoża na który spadnie− odbicia sprężyste/niesprężyste.

kerajs: Teoretycznie, przy zderzeniu niesprężystym, walec zawsze wbija się w podłoże pod jakimś kątem. Przypuszczam, że zderzenia są sprężyste, zważywszy na twardość monety i podłoża. A co z efektem żyroskopowym? Czy obrót wokół osi walca (lub w płaszczyźnie do niej prostopadłej) nie faworyzuje podstaw walca (powierzchni bocznej) ?

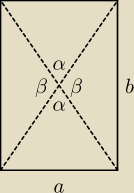
wredulus_pospolitus: Nie mogę się zgodzić z rozwiązaniem podanym przez @darasa. Załóżmy dla uproszczenia, że: 1) mamy standardową monetę o symetrycznym ułożeniu punktu ciężkości 2) zakładamy, że moneta spada 'na kant' w momencie gdy przy pierwotnym kontakcie z podłożem, kontakt ma kant a nie ścianka boczna monety. W tym momencie dla p=1/3 mamy:

	a√3
2(α + β) = 360o ; 2α = β −−−> α = 60o −−−> b = 2h = 2		= a√3 −−−>
	2

	a		√3
		=
	b		3

	r		a/2
pragnę zauważyć, ze dla		= √2 czyli przy moim oznaczeniu		= √2
	d		b

otrzymujemy monetę której kant jest ~2.82 większy od średnicy ściany bocznej

daras: Wyobraź sobie "dostatecznie" grubą monetę ale będącą jeszcze walcem. Sfera o prom. R opisana na walcu jest zbiorem zdarzeń elementarnych.

	1
Pole wycięte z powierzchni sfery przez pobocznicę walca ma być równe		pola sfery
	3

	2
stąd d =		R
	3

Podobno jeden student skleił ze sobą pięciogroszówki o średnicy 19,4 mm uzyskując rulon o

	r
grubości 6,7 mm (		≈1,44 ≈√2).
	d

Następnie upuszczał je z wysokości kilkunastu cm na miękki dywan czy wykładzinę uzyskując w serii 500 rzutów:176 orłów, 170 reszek i 154 "kanty" ≈ 31% Zainteresowanym mogę podać źródło. Podczas odbicia od twardego podłoża kant wypadał b.rzadko. Oczywiście można sobie wyobrazić takie rzuty, które polegałyby na "stawianiu" kantem upuszczanej monety z bardzo małej wysokości ale takie uważamy za fałszywe.

	r		1
Podobnie można też obliczyć		dla p=		.
	d		4

I'm back: Dokładnie daras − wycinek pola sfery ma być równe 1/3 całkowitemu polu sfery, czyli dla każdej z podstaw tego przekroju mamy mieć 1/6 pola sfery, związku z tym trójkąt o ramionach R i

	360
podstawie 2r ma mieć kat przy ramionach równy		= 60o, czyli 2r = R
	6

Związku z tym d = 2h_{trojkata równobocznego} = R√3

I'm back: Jeżeli d < R to kat pomiedzy ramionami w trójkącie o ramionach R i podstawie d będzie mniejszy niż 60^o więc pole wycinka będzie grubo mniejsze od 1/3 pola całej sfery. Kat ten powinien w tym trójkącie był równy 120^o (czyli trzecia część kąta pełnego)

Mila: Rzucać na śnieg.