Optymalizacja
Kamilla: Uzasadnić, że wśród graniastosłupów prawidłowych o podstawie sześciokątnej wpisanych w kulę o
promieniu r istnieje ten, który ma największą objętość.
Bardzo proszę o pomoc (najlepiej z rysunkiem).
Kamilla
5 cze 14:23
janek191:
a = r
H = 2 x − wysokość graniastosłupa
| | r2 √3 | |
V = Pp* H Pp = 6* |
| = 1,5 r2 √3 |
| | 4 | |
x
2 + r
2 = R
2 ⇒ x
2 = R
2 − r
2 ⇒ x =
√ R2 − r2
V = 1,5 r
2 √3*2
√R2 − r2 = 3
√3r
2*
√R2 − r2 = 3
√3 √ R2 r4 − r6
| | 3 √3*( 4 R2*r3 − 6 r5) | |
V ' (r) = |
| = 0 ⇔ 4 R2 r3 − 6 r5 = 0 /: |
| | 2√R2 r4 − r6 | |
r
3
4 R
2 = 6 r
2 / : 6
r
2 =
23 R
2
Dokończ.
5 cze 16:03
kerajs:
Skoro objętość ostrosłupa jest funkcją ciągłą o dodatnich wartościach, a dla wysokości bliskiej
0 lub 2R jest niemal zerowa, to istnieje wartość największa z tej funkcji. (Jeśli dodać
różniczkowalność tej funkcji na maksimum wskazuje tw. Rolla)
5 cze 17:34
Kamilla: Dziękuję. Janek191. Dokończyłam to zadanie. Zrobiłam założenia. Tabelkę przebiegu funkcji. I
dodatkowo policzyłam tę objętość.
Jest w porządku.
Ale mogłabym prosić o jakąś (poglądową) grafikę? Bo tak ciężko mi to sobie w głowie zobrazować.

5 cze 19:53
Kamilla: Kerajs. Również dziękuję za pomoc. Jednak bardziej chciałabym rozwiązać to zadanie na poziomie
szkoły średniej.
5 cze 19:55
Mila:
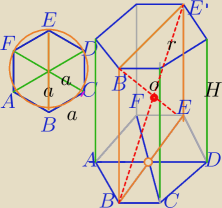
Rysunek.
|BE|=2a
|BE'|=2r
6 cze 18:48

 Rysunek.
|BE|=2a
|BE'|=2r
Rysunek.
|BE|=2a
|BE'|=2r