oblicz współczynnik kierunkowy prostej prostopadłej do prostej y=1
Student w potrzebie: Jaki jest współczynnik kierunkowy jakieś prostej prostopadłej do y=1?
wzór na prostopadłość to a1*a2=−1 ale skoro a1=0 to jakie jest a2?
W zadaniu też prosta prostopadła przechodzi przez (−2,6) ale ja mam problem jak wyznaczyć jej
ten współczynnik
Jakby ktoś pomógł byłbym wdzięczny
4 cze 18:35
σqa:
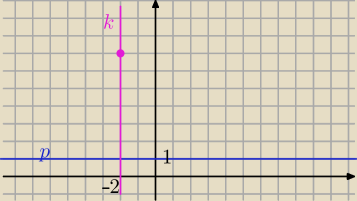
p: y=1
k⊥p to k: x= −2 bo P=(−2,6)∊k
4 cze 18:54
Student w potrzebie: Okej, to jest wynik, ale jak do niego dojść krok po kroku, można prosić o wytłumaczenie?
4 cze 19:08
Mila:
1) Równanie kierunkowe prostej
y=ax+b ,
wzór a1*a2=−1 dotyczy prostych, gdzie a≠0
Prosta y=1 ma równianie:
y=0x+b
W twoim przypadku należy kierować się wyobraźnią.
Po narysowaniu prostej y=1 widać, że jest nieskończenie wiele prostych prostopadłych do
niej.
W zadaniu masz podany warunek − prosta przechodzi przez punkt A=(−2,6) i 18:54 masz
ilustrację.
2)
Jeżeli prosta jest podana równaniem ogólnym:
Ax+By+C=0
to prostopadła do niej ma wzór:
Bx−Ay+D=0
czyli w Twoim przypadku:
m: y=1 ( czyli 0x+y+0=0, A=0, B=1, C=0)
1x+D=0
1*(−2)+D=0 − bo prosta przechodzi przez punkt A
D=2
n:x+2=0⇔x=−2
n⊥m
4 cze 19:29
σqa:

4 cze 19:40
Mariusz :
Aby wyprowadzić warunek prostopadłości prostych dla postaci kierunkowej
wystarczy skorzystać z tego że tangens kąta nachylenia prostej do osi odciętych
jest równy współczynnikowi kierunkowemu prostej oraz ze wzoru na tangensa różnicy kątów
Teraz wystarczy zaobserwować co się dzieje z tangensem
jeżeli kąt między prostymi będzie dążył do kąta 90°
Będzie miało to miejsce wtedy gdy mianownik tego tangensa różnicy kątów będzie równy zero
W przypadku równania ogólnego prostej przydatna będzie wartość cosinusa kąta między prostymi
Jeżeli znasz wektory to wartość tego cosinusa dostaniesz z iloczynu skalarnego
Masz proste o równaniach ogólnych
A
1x+B
1y+C
1=0
A
2x+B
2y+C
2=0
Tworzysz sobie wektory
v
1 = [A
1 , B
1]
v
2 = [A
2 , B
2]
Z jednej strony iloczyn skalarny to
A
1A
2 + B
1B
2
Z drugiej strony iloczyn skalarny to
|v
1|v
2|cos(∡v
1v
2)
Masz zatem
A
1A
2 + B
1B
2=|v
1|v
2|cos(∡v
1v
2)
A
1A
2 + B
1B
2=
√A12+B12√A22+B22cos(∡v
1v
2)
| | A1A2 + B1B2 | |
cos(∡v1v2)= |
| |
| | √A12+B12√A22+B22 | |
A ile wynosi cosinus kąta 90° ?
4 cze 22:36
 p: y=1
k⊥p to k: x= −2 bo P=(−2,6)∊k
p: y=1
k⊥p to k: x= −2 bo P=(−2,6)∊k
