Działania na logarytmach Ola: Cześć, mam problem z zadaniem log_3√2 (¹₃₆) − log_3√2 (9) =

Szkolniak:

	1
log3√2(		)−log3√2(9)=−log3√2(36)−log3√2(9)=
	36

	log3(22*34)
=−log3√2(36*9)=−		=
	log3(3√2)

	log3(22)+log3(34)
=−		=
	log3(3)+log3(√2)

	2log3(2)+4
=−		=
	1   1+ log3(2)   2

	4(log3(2)+2)
=−		=−4
	2+log3(2)

Eta: 3√2=√18 =18^1/2 i 36*9=324=18² =

	1
.......= log181/2(		) = log181/2 (18−2) = −4
	36*9

Eta:

Ola: Już rozumiem. Dziękuję bardzo za pomoc

Ola: Trapez równoramienny ABCD wpisano w okrąg tak, że dłuższa podstawa jest średnicą tego okręgu.

	3
Stosunek obwodu trapezu do sumy długości jego podstaw wynosi		.
	2

Oblicz cosinus kąta ostrego trapezu .

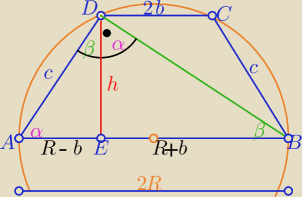
Eta: |AE|=R−b , |EB|=R+b , b<R z treści zad.

	2c+2b+2R		3		c		3
		=		⇒		+1=		⇒ R+b=2c
	2b+2R		2		R+b		2

z podob. trójkątów AED i DEB ( kk) h²=|AE|*|EB| h²=(R−b)*2c / : c²≠0

	h		R−b
(		)2=2(		) ⇒ sin2α=2cosα
	c		c

otrzymamy : cos²α+2cosα−1=0 Δ=8 i cosα>0 ............................. cosα=√2−1 ==========

Mila: