Hiperbola anonim123: Jak wyznaczyć długości półosi hiperboli współrzędne ognisk mimośród równania kierownic I asymptot jeżeli hiperbola jest przesunięta względem układu współrzędnych Tak jak w tym przypadku https://zapodaj.net/47496f1b11241.jpg.html Jest to podpunkt d)

anonim123:

(x−1)2		(y+3)2
	−		=1 to jest równanie hiperboli o które mi chodzi
4		9

anonim123: ?

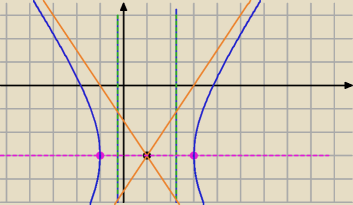
Mila: S=(1,−3)− środek hiperboli 1) a=2, b=3 c²=a²+b²⇔c²=13 c=√13 2) F₁=(1−√3,−3), F₂=(1+√3,−3) 3)

	c		√13
e=		=
	a		2

4) Kierownice:

	4
x=±		+1
	√13

anonim123: a skąd się wzięły te ogniska?

anonim123: a następne podpunkty są ze wzorów czy trochę zmodyfikowane?

□: 1) c=±√13

	x2		y2
(0,0) środek dla hiperboli		−		=1
	4		9

(−√3,0) i (−√3.0) (1,−3) − środek dla danej hiperboli na początku (0,0) przesunięto o wektor [1,−3] Ogniska przesuwamy o wektor [1,0] ( w poziomie ) y=−3 oś symetrii F₁=(−√3+1,−3) F₂=(√3+1,−3)

Mila: wzory: https://www.youtube.com/watch?v=PefdTu5okc8