Całki podwójne, współrzędne biegunowe Szkolniak: Wprowadzając współrzędne biegunowe obliczyć podane całki podwójne po wskazanych obszarach:

	x
Mam taki obszar: x2+y2≤1,		≤y≤√3x, podstawiam pod x=rcos(α) oraz pod y=rsin(α) i
	√3

wychodzi mi, że:

	cos(α)
r2≤1 oraz		≤sin(α)≤√3cos(α)
	√3

'r' jest w zakresie od 0 do 1, natomiast jak wyznaczyć zakres kąta alfa? bo trochę tego nie rozumiem

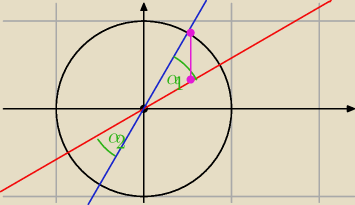
Saizou : I metoda

	√3		π
czerwony wykres to y =		x → kąt nachylenia prostej to
	3		6

	π
niebieski to wykres y = √3x → kąt nachylenia prostej to		,
	3

	π		π
czyli α1 zmienia się w zakresie [		;		]
	6		3

Można określi jeszcze zakres α₂, albo przemnożyć całkę przez 2. II metoda Masz do rozwiązania układ nierówności

1
	*rcosa ≤ rsina
√3

rsina ≤ √3*rsina

Szkolniak: Ciekawa ta pierwsza metoda, drugą metodą właśnie teraz rozwiązałem i wyszedł mi również

	π		π
przedział [		;		]
	6		3

A mam jeszcze jedno pytanie, jeszcze jeden obszar: 1) x≥0 , 1≤x²+y²≤2 : czy tutaj r∊[1;√2]? i alfę jak? patrząc na wykres funkcji cosinus to

	π		3
próbowałbym to zapisać jako α∊[0;		]∪[		π;2π], ale niezbyt rozumiem
	2		2

Saizou :

	π
α ∊ [0;		]
	2

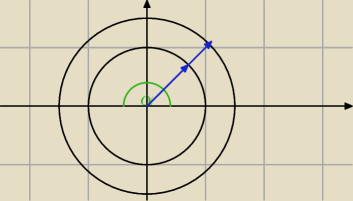
r ∊ [1; √2] całkę przemnóż przez 2

Saizou :

	π		π
możesz też zrobić przedział [−		;		]
	2		2

Szkolniak: Saizou właśnie dzisiaj rano wpadłem na pomysł żeby wziąć jeden z przedziałów i pomnożyć razy dwa no nic, dzięki za pomoc, trzeba potrenować tę zamianę na współrzędne biegunowe