trójkąt stosunek odcinków Szafira: W trójkącie ABC poprowadzono środkową CD oraz odcinek AE, który podzielił bok BC w stosunku 4:1 licząc od wierzchołka B. Odcinki te przecinają się w punkcie P. Wyznacz stosunek długości |AP| : |PE|. Proszę o pomoc w rozwiązaniu zadania.

mn: |AP| : |PE|=5:1

Szafira: @mn a mogłabym poprosić o opis rozwiązania jaki Cie do tego doprowadził?

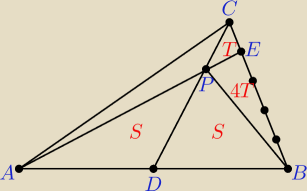
magik: Pola trójkątów: P_ADP = P_DBP = S i P_BEP = 4P_PEC = 4T P_ADP + P_APC = P_DBP + 4P_PEC + P_PEC ⇒ S + P_APC = S + 5T zatem P_APC = 5T ⇒ |AP| = 5|PE|

Szafira: Dziękuje <3

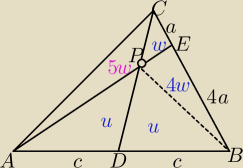
mn: P_ADC=P_BDC P_BDC= 5w+u to P_APC=5w zatem |AP| : |PE| = 5 : 1 Pozdrawiam "magika"