Pomocy pilne!
Emilka: Witam potrzebuję pomocy z tym zadaniem, a dokładnie ze zrozumieniem jego rozwiązania.
Treść:
Podstawy trapezu równoramiennego mają długość 12 i 16, a jego wysokość jest równa 14.
Oblicz promień okręgu opisanego na tym trapezie.
Rozwiązanie:
a=dł. dłuzszej podstawy=16
b= dł. krótszej=12
h=14
a=b+2x
16=12+2x
x=[16−12]/2=2
c= dł. ramienia
z pitagorasa;
h²+x²=c²
14²+2²=c²
c=√200=10√2
szukany promien to promień okregu opisanego na trójkacie;
podstawa, ramię, przekatna
d= przekatna
d=√[14²+14²]=√392=14√2
AB= DŁUZSZA PODSTAWA
CD= KRÓTSZA
pole Δ ABC=1/2*16*14=112
R= szukany promień
R= a*c*d / 4 pola=16*14√2*10√2 / 4*112=4480/448=10
Mógłby ktoś zrobić rysunek i opisać za co odpowiadają te obliczenia?
Muszę zrozumieć na czym dokładnie polega to rozwiązanie krok po kroku.
Z góry dziękuje za pomoc.
23 maj 16:52
Mila:
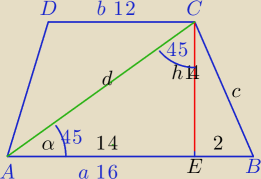
1)
|EB|=(16−12):2=2
|AE|=14⇔ΔAEC− Δprostokątny równoramienny
α=45
o
d=14
√2
2) W ΔCEB:
c
2=14
2+2
2
c
2=200⇔c=10
√2
3) Z tw. sinusów
R=10
==========
Twoje obliczenia w drugiej części są takie:
1) obliczasz P
ΔABC
2) Aby obliczyć promień okręgu opisanego na ΔABC
( jednocześnie jest to promień okręgu opisanego na trapezie ABCD)
korzystasz z wzoru
Jeśli masz pytanie to pisz.
23 maj 18:53
 1)
|EB|=(16−12):2=2
|AE|=14⇔ΔAEC− Δprostokątny równoramienny
α=45o
d=14√2
2) W ΔCEB:
c2=142+22
c2=200⇔c=10√2
3) Z tw. sinusów
1)
|EB|=(16−12):2=2
|AE|=14⇔ΔAEC− Δprostokątny równoramienny
α=45o
d=14√2
2) W ΔCEB:
c2=142+22
c2=200⇔c=10√2
3) Z tw. sinusów