Liczba partii Mat: Czy dobrze myślę, że wzór na liczbę przekątnych nijak ma się do liczby rozegranych partii, chyba że mielibyśmy policzyć ilość możliwych partii bez zagrania ze swoimi osobami z drużyny jeśli liczy ona 3 osoby? Z własności wielokątów Inne pytanie, jak obliczyć ilość możliwych rozegranych partii w grupie 4 osób, jeśli każdy może zagrać max dwie partie?

Mat: A dobra, dla 4 osób nie może tak być bo zawsze zostanie jedna osoba, która zagra jedną partię

Mat: Chociaż chyba tak być nie może* albo jedną osoba w ogóle nie zagra albo wszystkie zagrają dokładnie dwie 12, 13, 23 lub 12, 14, 23, 34, zatem jak to obliczyć bez rozpisywania?

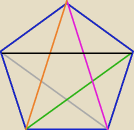
Mila: 1) n=5 − pięć wierzchołków (boków) Liczba przekątnych:

5 2
	−5=10−5=10

5 2
	− liczba odcinków , jesli masz 5 punktów z których żadne trzy nie są współliniowe.

Odejmujesz 5 , bo boki nie są przekątnymi 2) n=6

6 2
	−6=9

3) Wzór : n− liczba boków wielokąta wypukłego

n 2
	−n − liczba przekątnych

Po przekształceniu:

n*(n−1)		n*(n−3)
	−n=
2		2

Mat: To rozumiem, chodziło mi o wzór dla np ilości rozegrania partii jeśli każdy ma rozegrać dwie, trzy itd dla n osób

Mila: n− liczba osób 1) Gra każdy z każdym jedną partię bez rewanżu: wzór :

n 2		n*(n−1)
	=		− liczba rozgrywek
		2

2) Gra każdy z każdym jedną partię z rewanżem. n*(n−1)− liczba rozgrywek O to Ci chodziło?