geometria
Trebuh:
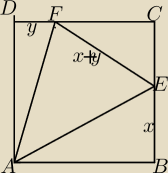
W kwadracie 𝐴𝐵𝐶𝐷 wybieramy na boku 𝐵𝐶 taki punkt 𝐸, a na ++boku 𝐶𝐷 taki punkt 𝐹, że
|𝐸𝐹| = |𝐵𝐸| + |𝐹𝐷|. Udowodnij, że kąt
𝐸𝐴𝐹 ma 45 stopni.
22 maj 17:57
Eta:
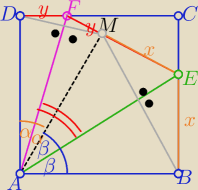
Punkt D i punkt B odbijamy symetrycznie odpowiednio względem prostej AF i AE
otrzymując punkt M co daje warunek |EF|=x+y
w wyniku otrzymujemy dwa deltoidy
zatem 2α+2β=90
o ⇒ α+β=45
o
|∡EAF|=α+β=45
o
===============
22 maj 20:19
Mila:
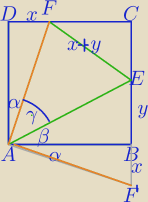
II sposób
ΔAF'E≡ΔAEF ⇔
γ=α+β
2(α+β)=90
o (∡DAB)
α+β=45
o
γ=45
o
====
22 maj 21:08
.:
22 maj 21:47
Trebuh:
Dlaczego kolorowe trójkąty są przystające?
23 maj 00:30
to i to:
Dlatego,że są
kolorowe 
23 maj 01:19
Mila:
ΔABF'≡ΔADF (DORYSOWANY)
|AF'|=|AF|
AE−wspólny bok dla ΔAFE i ΔAEF
|FE|=x+y=|EF'|
ΔAFE ≡ΔAEF − cecha bbb
23 maj 15:40
 W kwadracie 𝐴𝐵𝐶𝐷 wybieramy na boku 𝐵𝐶 taki punkt 𝐸, a na ++boku 𝐶𝐷 taki punkt 𝐹, że
|𝐸𝐹| = |𝐵𝐸| + |𝐹𝐷|. Udowodnij, że kąt
𝐸𝐴𝐹 ma 45 stopni.
W kwadracie 𝐴𝐵𝐶𝐷 wybieramy na boku 𝐵𝐶 taki punkt 𝐸, a na ++boku 𝐶𝐷 taki punkt 𝐹, że
|𝐸𝐹| = |𝐵𝐸| + |𝐹𝐷|. Udowodnij, że kąt
𝐸𝐴𝐹 ma 45 stopni.
 Punkt D i punkt B odbijamy symetrycznie odpowiednio względem prostej AF i AE
otrzymując punkt M co daje warunek |EF|=x+y
w wyniku otrzymujemy dwa deltoidy
zatem 2α+2β=90o ⇒ α+β=45o
|∡EAF|=α+β=45o
===============
Punkt D i punkt B odbijamy symetrycznie odpowiednio względem prostej AF i AE
otrzymując punkt M co daje warunek |EF|=x+y
w wyniku otrzymujemy dwa deltoidy
zatem 2α+2β=90o ⇒ α+β=45o
|∡EAF|=α+β=45o
===============
 II sposób
ΔAF'E≡ΔAEF ⇔
γ=α+β
2(α+β)=90o (∡DAB)
α+β=45o
γ=45o
====
II sposób
ΔAF'E≡ΔAEF ⇔
γ=α+β
2(α+β)=90o (∡DAB)
α+β=45o
γ=45o
====
