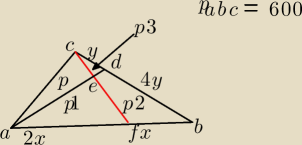
 Dostałem takie zadanko, bez żadnej treści. Mam obliczyć pole P. Próbowałem to rozwiązać.
Zacząłem tak:
6003x=Pacf2x
1200x=3x*Pacf
400=Pacf
Pbcf= Pabc − Pacf = 600 − 400 = 200
P + P1 = 400
P2+ P3 = 200
Wiem, że trzeba podzielić czworokąt BDEF na dwie części przekątną ale nie jestem do końca
pewien jak to będzie.
I dalej się zaciąłem. Proszę o pomoc.
Dostałem takie zadanko, bez żadnej treści. Mam obliczyć pole P. Próbowałem to rozwiązać.
Zacząłem tak:
6003x=Pacf2x
1200x=3x*Pacf
400=Pacf
Pbcf= Pabc − Pacf = 600 − 400 = 200
P + P1 = 400
P2+ P3 = 200
Wiem, że trzeba podzielić czworokąt BDEF na dwie części przekątną ale nie jestem do końca
pewien jak to będzie.
I dalej się zaciąłem. Proszę o pomoc.
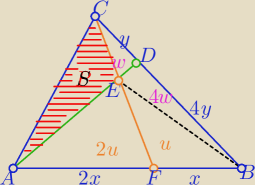 w , u , 4w, 2u, S −−−− to pola odpowiednich trójkatów
P(ABC)= S+5w+3u =600
w , u , 4w, 2u, S −−−− to pola odpowiednich trójkatów
P(ABC)= S+5w+3u =600
| S | ||
w ΔAFC i BFC : S+2u=2(5w+u) ⇒ S=10w ⇒ 5w= | ||
| 2 |
| S | ||
zatem : P(ABC)= S+ | +4S=600 | |
| 2 |
| 1 | ||
S= 109 | ||
| 11 |
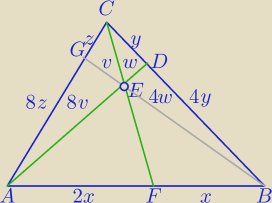 II sposób.
1)
Z Tw. Cevy:
II sposób.
1)
Z Tw. Cevy:
| |CG| | 2x | 4y | |||
* | * | =1 | |||
| |G|A | x | y |
| |CG| | 1 | ||
= | |||
| |GA| | 8 |
| 600 | ||
(*) v+5w= | ||
| 9 |
| PΔAEC | 2x | ||
= | ⇔ | ||
| PΔCEB | x |
| 9v | ||
3) | =2 | |
| 5w |
| 9 | ||
9v=10w⇔w= | v | |
| 10 |
| 9 | 200 | |||
v+5* | v= | |||
| 10 | 3 |
| 1200 | ||
9v=PΔAEC= | ||
| 11 |