Geometria, dowodzenie Alaias: Przekątne trapezu ABCD ( AB równoległe do CD) przecinają się w punkcie E. Okręgi opisane na Δ AED i Δ BCE przecinają się w punkcie F należącym do boku AB. Wykaż, że CF=DF

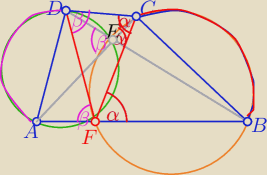
Eta: Rysunek sporządź samodzielnie ( bo w tym edytorze nie mogę go narysować ∡BFC=∡FCD =α jako naprzemianległe oraz ∡BEC=α −− jako wpisany w okrąg i oparty na tym samym łuku BC analogicznie ∡FAC=∡FDC=β −− naprzemianległe oraz ∡AED=β −− jako wpisany w okrąg oparty nałuku AD oraz ∡AED=∡BEC−− jako wierrzcołkowe zatem β=α to ΔFDC jest równoramienny to ramiona |FC|=|FD| co kończy dowód

Eta:

Alaias: Dzięki, super