Dany jest zworokat ABCD, który nie ma par boków rownolegtych. Matma: Dany jest zworokat ABCD, który nie ma par boków rownolegtych. Punkt K jest stodkiem boku AB , a punkt L jest srodkiem boku CD. Natomiast punkty M i N sa odpowiednio srodkami przekatnych AC i BD. Wykaz, Ze NL |I MK.

wmboczek: MK || CD i LN || CD na podstawie tw. Talesa

Matma: A mogłabym krok po kroku

Matma: Bo wiem ze tw Talesa

wredulus_pospolitus: 1) zrób rysunek 2) zaznacz trójkąty DNL oraz DBC zauważ, że są podobne (podobieństwo BKB) 3) analogicznie dla AMK i ABC 4) z podobieństwa wynika, że NL || BC oraz MK || BC związku z tym NL || MK Korzystanie z tw. Talesa nie jest do końca prawidłowym podejściem, bo aby z tego twierdzenia skorzystać musimy najpierw założyć równoległość tych odcinków z bokiem BC, a z tego wynika będzie proporcja długości boków/przekątnych. My natomiast idziemy 'odwrotną drogą'. Wiemy, że istnieje proporcja i z tego wykazujemy równoległość (dzięki podobieństwo trójkątów).

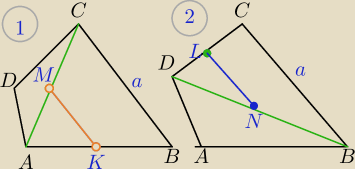
Mila: Wiadomości: Odcinek łączący środki dwóch boków trójkąta jest równy połowie trzeciego boku i równoległy do niego. 1) Rys. 1 MK− odcinek łączący środki boków ΔCAB⇔

	1
MK||BC ( i |MK|=		a)
	2

Rys. 2 LN− odcinek łączący środki boków ΔCDB⇔ LN||BC 2) Z (1 i 2)⇒MK||LN