Dany jest sześcian ABCDEF GH o krawędzi długości 2. Punkt P jest środkiem kraw Matma: Dany jest sześcian ABCDEF GH o krawędzi długości 2. Punkt P jest środkiem krawędzi BC . Płaszczyzna AHP przecina krawędź CG w punkcie R (zobacz rysunek). Oblicz pole przekroju tego sześcianu płaszczyzną przechodzącą przez punkty A ,H ,R i P . Czy mógłby mi ktoś wytłumaczyć czemu APRh jest trapezowym równoramiennym

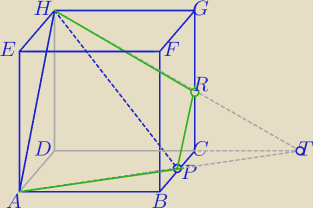
Mila: Czy rysunek przekroju wyjaśnia problem?

Matma: Tak, a jak bym mogła to na maturze napisać dlaczego jest równoramienny?

Mila: 1) AH||PR 2) ΔABP≡ΔHGR⇔|HR|=|AP|