planimetria jendrzej: Dany jest trapez ABCD o obwodzie l i podstawach AB i CD takich że, |AB|>|CD|. Trapez jest opisany na okręgu i wpisany w okrąg, a przekątna AC trapezu ma długość d. Wykaż źe promień R okręgu opisanego na trapezie ABCD jest równy

	dl
R=
	2√16d2−l2

(Podstawa AB nie zawiera środka okręgu opisanego)

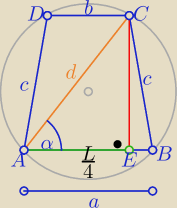marysia: Taki trapez jest równoramienny

	a+b
to |AE|=
	2

	a+b
z warunku wpisania okręgu w trapez : a+b=2c , c=
	2

	L		a+b
to L=4c ⇒ c=		=
	4		2

	L		√16d2−L2
w ΔAEC : cosα=		to sinα= √1−cos2α=
	4d		4d

	c
z tw. sinusów 2R=
	sinα

..................

	Ld
R=
	2√16d2−L2

===============

jendrzej: marysia: Bardzo dziękuję