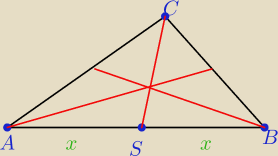
Wykaż,że PATMAT16: Dany jest trójkąt ABC. Punkt S jest środkiem boku AB tego trójkąta. Wykaż, że odległości punktów A i B od prostej CS są równe. Da się to wykazać ze środkowych? Ja to oznaczyłem tak:

wredulus_pospolitus: I co później chcesz z tymi środkowymi zrobić Nawet jeżeli by się dało ... to po co sobie utrudniać życie

chichi: Niech O będzie pkt. przecięcia się środkowych, |SO| = y, h_A oraz h_B będą wysokościami opuszczonymi na bok SO (lub jego przedłużenie) odpowiednio z wierzchołka A i B, wówczas:

	yhA		yhB
PASO = PSBO ∧ PASO =		∧ PSBO =		⇔ hA = hB □
	2		2

Jak poprowadzimy środkowe to mamy 6 trójkątów o jednakowych polach ↑ tam to wykorzystałem

chichi: II sposób to opuścić te wysokości i pokazać błyskawicznie przystawienie trójkątów prostokątnych

PATMAT16: Dziękuję