trójkąt Luis: Dany trójkąt ABC o bokach 15,20,25. Oblicz odległość między środkiem okręgu wpisanego a środkiem okręgu wpisanego w trójkąt o wierzchołkami w środkach boków trójkąta ABC.

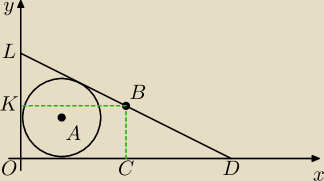
getin: Jest to trójkąt prostokątny, bo 15²+20²=25² a=15 b=20 c=25

	a+b−c
r =		= 5
	2

A(5;5) B − środek okręgu opisanego na trójkącie prostokątnym jest w połowie przeciwprostokątnej B − środek LD, gdzie L(0;15) oraz D(20;0) zatem B(10; 7,5)

	5√5
|AB| = √(10−5)2+(7,5−5)2 = √25+6,25 = √31,25 =
	2

Eta: Z tw. Eulera d²=R²−2Rr ==========

	25
w trójkącie prostokątnym : R=		, 2r=20+15−25=10
	2

	5√5
d=
	2

==========

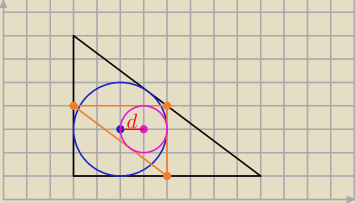
Saizou : Tylko, że w zadaniu nie chodzi o okrąg opisany na trójkącie ABC a o okrąg wpisany w trójkąt o wierzchołkach położonych w połowie długości boków trójkąta ABC. d = 5 − 2,5 = 2,5

getin: a rzeczywiście masz rację, nie doczytałem

getin: ale swoją drogą to jest dziwna treść zadania, w sumie to nie wiadomo do końca co trzeba wyliczyć