Prawdopodobieństwo yn:

	2		1
O zdarzeniach A, B ⊂ Ω wiadomo, że 𝑃(𝐴) =		, 𝑃(𝐵 ′) =		, 𝑃(𝐴′ ∩ 𝐵′) =
	3		6

	5
		. Oblicz 𝑃(𝐴 ∩ 𝐵).
	12

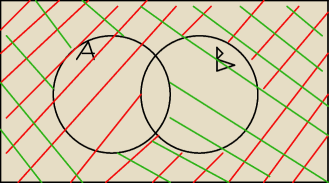
Kolorem czerwonym zaznaczyłam 𝑃(𝐵′), a kolorem zielonym 𝑃(𝐴'). Z rysunku zauważyłam, że: 𝑃(𝐴 ∩ 𝐵) = 1 − 𝑃(𝐴′ ∪ 𝐵′)

	2		1
𝑃(𝐴') = 1 −		=
	3		3

	1		1		5		1
𝑃(𝐴′ ∪ 𝐵′) = 𝑃(𝐴') + 𝑃(𝐵′) − 𝑃(𝐴′ ∩ 𝐵′) =		+		−		=
	3		6		12		12

	1		11
𝑃(𝐴 ∩ 𝐵) = 1 − 𝑃(𝐴′ ∪ 𝐵′) = 1 −		=
	12		12

A odpowiedź to: 𝑁𝑖𝑒 𝑖𝑠𝑡𝑛𝑖𝑒𝑗𝑒 𝑡𝑎𝑘𝑖𝑒 𝑃(𝐴 ∩ 𝐵). Czy ktoś mógłby wytłumaczyć co zrobiłam źle?

getin: Nie sprawdziłaś czy spełniony jest warunek konieczny istnienia P(A∩B) czyli chociażby P(A) ≥ P(A∩B). Zbiór A musi mieć co najmniej tyle samo elementów niż część wspólna zbiorów A i B Tutaj to nie zachodzi więc stąd bierze się sprzeczność i brak rozwiązania

yn: Rzeczywiście, dziękuję