Trójkąt Pascala PATMAT16: Jak rozwiązać to zadanie trójkątem Pascala? Po przekształceniu wyrażenia algebraicznego (x√2+y√3)⁴ do postaci: ax⁴+bx³y+cx²y²+dxy³+ey⁴

PATMAT16: Prosiłbym w miarę możliwosci o wytłumaczenie. Wiem, że ten trójkąt ma wyglądać tak. Rozumiem działania na liczbach, ale nie rozumiem ich zapisu (Dlaczego jedynki, skąd się bierze dwójka , potem dwie trójki i 4 6 4.Wynikiem jest 36 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1

Eta: https://pl.wikipedia.org/wiki/Dwumian_Newtona

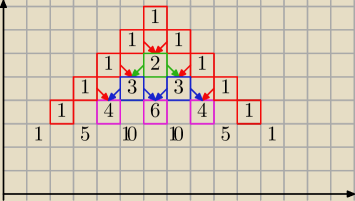
Saizou : Te liczby to sumy sąsiadujących liczb np. (zobacz rysunek). Liczby stojące w n−tym wierszu to kolejne współczynniki dwumianu Newtona rozwinięcia (a+b)ⁿ, np. (a+b)³ = 1*a³+3*a²b+3*ab²+1*b³. Ze wzoru dwumianowego Newtona mamy

	3 0		3 1		3 2		3 3
(a+b)3 =		*a3b0 +		*a2*b1 +		*a1*b2 +		a0*b3

Jak można zauważyć, trójkąt Pascala posłużył do wyliczenia symbolów Newtona. U Ciebie w zadaniu są jeszcze współczynniki stojąca przy x oraz y, które należy podnosić do odpowiednich potęg. (√2x+√3y)⁴ = 1*(√2x)⁴ + 4*(√2x)³*√3y + 6*(√2x)²*(√3y)² + 4*√2x*(√3y)³ + 1*(√3y)⁴

PATMAT16: Dobrze, już rozumiem jak to działa, tylko skąd mam wiedzieć potęga którego stopnia przy czym stoi? Nie mówię tutaj o (√2x)⁴ , bo na krańcu to oczywiste, że do potęgi czwartej. Co z 4*(√2x)³*(√3y)? Da się odczytać jakoś tę potęgę, że to będzie akurat trzeci stopień z tego trójkąta?

Saizou : Potęgi maleją lub rosną. (x+y)⁴ = x⁴y⁰ + 4x³y¹ + 6x²y² + 4x¹y³ + x⁰y⁴ zauważ też, że suma potęg jest zawsze równa 4 4+0 = 4 3+1 = 4 2+2 = 4 1+3 = 4 0+4 = 4

PATMAT16: Dziękuję bardzo!