Planimetria Sinusik: W trójkącie równobocznym ABC na boku AB zaznaczono punkt D w taki sposób, że AD : DB = 1: 3 . Wyznacz sinus kąta BCD.

Eta:

	1
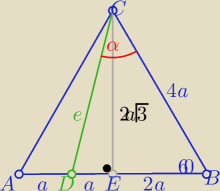
P(DBC)=		*3a*4a*sin60o= 3a2√3
	2

	1
P(DBC)=		*e*4a*sinα
	2

e= √12a²+a² = a√13 Porównaj pola i wyznacz sinα=.........

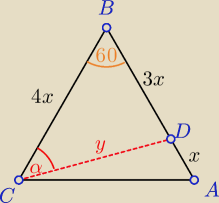xyz: z tw. cosinusow: 1) y² = (4x)² + (3x)² − 2*4x*3x*cos(60) = 13x² 2) (3x)² = (4x)² + y² − 2*4x*y*cos(α) 9x² = 16x² + 13x² − 2*4x*x√13*cos(α) 20x² = 8x²√13cosα

20
	= √13cos(α)
8

	20
cos(α) =
	8√13

sin(α) = √1−cos²α = ...

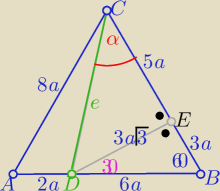Eta: To jeszcze taki sposób: Z własności ΔDBE "ekierkowego" o kątach ostrych 30^,60^o e=√25a²+27a²= a√52= 2a√13

	3a√3
sinα=
	2a√13

	2√39
sinα=
	26

============

Eta:

	3√39
sinα=
	26