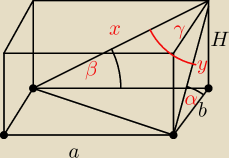
Oblicz kąt między przekątnymi sąsiednich ścian bocznych
poprowadzonymi z jednego wierzchołka w graniastosłupie prostym o
podstawie prostokąta wiedząc, że są one (przekątne) nachylone do płaszczyzny podstawy
pod kątem α oraz β.
1) cosα=by
2) cosβ=ax
3) H2+b2=y2
4) H2+a2=x2
5) a2+b2=x2+y2−2xycosγ
Jak znaleźć 5 równanie do układu?
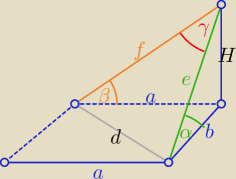b=H*ctgα , a=H*ctgβ , e=H/sinα , f=H/sinβ
| cos2α | cos2β | |||
i d2=a2+b2= H2( ctg2β+ctg2α) = H2( | + | ) | ||
| sin2α | sin2β |
| f2+e2−d2 | ||
cosγ= | podstaw dane... i ( upraszcza się H2 | |
| 2ef |
| 1 | 1−cos2α | 1−cos2β | ||||
cosγ= | ( | + | )*sinα*sinβ | |||
| 2 | sin2α | sin2β |
