przygotowanie do konkursu z geometri
agniesia:
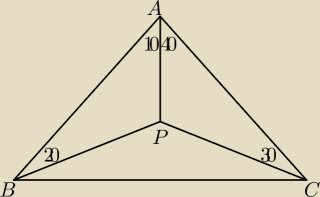
Przygotowuje sie do konkursu z geometri i polecenie jest takie
Pokaz ze trojkat ABC jest rownoramienny wykorzystujac jedynie zasady geometri syntetycznej (bez
uzycia metod algebrainczych). Prosze o odpowiedz albo naprowadzenie
28 kwi 01:04
Mila:
Czy taka jest treść, czy może sama narysowałaś ten Δ?
28 kwi 21:56
Eta:
Myślę,że
agnisia to nasz "małolat"

29 kwi 21:29
wredulus_pospolitus:
Drogie Panie, a ja mam takie oto pytanie:
Czy z faktu, że ∡BPC = 2*∡BAC mamy jednoznacznie powiedzieć, że punkt P jest środkiem okręgu
opisanego na ΔABC ?
Jeżeli tak to ... to nie jest trójkąt równoramienny.
29 kwi 22:39
Eta:
Dokładnie taaaak

29 kwi 22:48
Eta:
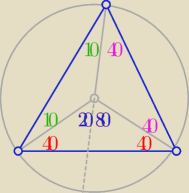
Ale wtedy na rys. powinno być tak
A tak nie jest
więc coś nie ... halo

29 kwi 23:00
ite:
Gdyby autorem pytania był użytkownik, o którym mowa o 21:29, to byłoby to zadanie z geometryi z
podręcznika dla szkół powszechnych siedmioklasowych.
A tu jest po prostu z "geometri".
29 kwi 23:30
Mila:
Najlepiej, aby autor napisał treść zadania, rysunek to za mało.
Znalazłam takie zadanie− też chodzi o Synthetic solution.
Consider ΔABC and a point M in its interior so that ∠MAB=10∘,∠MBA=20∘
,∠MCA=30∘ and ∠MAC=40∘. What is ∠MBC?
30 kwi 00:08
Mila:
Nie należy (chyba) pisać rozwiązania, zastrzeżone są prawa autorskie.
Strona : "Zawody matematyczne amerykańskiego stowarzyszenia".
Powyższe zadanie( 00:08 ) znalazłam gdzie indziej.
Może ktoś biegły w angielskim doczyta o co chodzi z tymi prawami. Tłumaczenie nie jest dla mnie
jasne.
Rozwiązanie zadania z 20 kwietnia i 30 kwietnia metodą syntetyczną jest proste.
Jeśli agniesia się zgłosi to napiszę podpowiedź.
2 maj 23:29
Kacper:
To zadanie z 1996 roku z amerykańskiej olimpiady matematycznej

20 maj 19:59
Mila:
Zgadza się.Rozwiązujemy?
20 maj 20:21
Min. Edukacji: Ale tylko za $😄
20 maj 21:07
Kacper:
Mila myślę, że nie jest to zakazane

Ja z trygonometrii mam pomysł, ale wiadomo, że najładniejsze są rozwiązania syntetyczne

21 maj 11:02
Mila:
Kacper
Ja mam rozwiązanie bez trygonometrii.
1)
Przedłużyć BP.
2)
Z punktu A poprowadzić półprostą AK, aby |∡ PAK |=10o, K∊półprostej BP.
Otrzymasz Δ równoramienny BKA. Dalej zobaczysz.
Trudno mi zrobić dobry rysunek.
Postaram się zrobić, a może Ite tu spojrzy i w geogebrze zrobi.
21 maj 14:56
chichi:
Wg mnie trzeba mieć naprawdę ograniczoną wyobraźnię żeby nie widzieć tutaj syntetycznych
rozwiązań

22 maj 00:40
maja:
nadajesz się na wykładowcę, arogancja i wyższość nad innymi... i obrażanie
22 maj 08:46
Mariusz:
Maja ja już dawno to zauważyłem
On jest jeszcze bardzo młody ale raczej z tego nie wyrośnie
22 maj 12:40
23 maj 15:59
ite:
oznaczenia dałam z treści 30 kwi 00:08, ale może zmienić?
23 maj 16:02
Trebuh:
Czy mógłbym prosić o pomoc w rozwiązaniu?
23 maj 17:27
Mila:
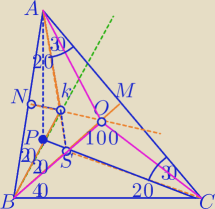
Podpowiedź
1) rysunek
2)
O − punkt przecięcia symetralnych boków Δ ( środek okręgu opisanego na ΔABC)
ΔAKB− Δrównoramienny (20,20 ,140)
ΔΔASC −Δrównoramienny (30, 30,120)
23 maj 18:31
Mila:
Dziękuję ite , może w geogebrze da się lepiej narysować.
Czy widzisz luki w rozwiązaniu?
Kacper ma rozwiązanie z trygonometrią. Może napisze?
23 maj 18:33
chichi:
@
Mila to Twoje czy zapożyczone?

23 maj 19:25
Trebuh: Miła bardzo dziękuję za pomoc, będę analizować.
Pan chichi potrafi tylko wystawiać język i upominać innych czy rozwiązać też?
23 maj 19:44
Mila:
Tak , zapożyczone od Ciebie chichi, Pegasus mi pomógł.
23 maj 20:12
Trebuh: Dlaczego prosta SM przechodzi przez B? Z czego to wynika?
24 maj 00:50
Mila:
O− środek okręgu opisanego na ΔABC ( punkt przecięcia symetralnych boków Δ)
|BO|=|AO|=|CO|=R
∡BOC, ∡A − kąt środkowy i wpisany oparty na cięciwie AB
|∡BOC |=2*50o=100o
ΔBOC− Δrównoramienny ( 100o,40o,40o)
2)
ΔAOC− Δrównoramienny o katach (10o,10o,160o)
|∡AOC|=160o⇒|∡ABC|=80o kąty : środkowy i wpisany oparte na cięciwie AC
3)
|∡BCA|=50o
Teraz widzisz wszystko?
Nie mogłam dobrego rysunku zrobić z okręgiem.
Można jeszcze inaczej wyjaśnić. Zostawiam do przemyślenia.
Jeśli Kacper nie napisze rozwiązania z trygonometrią, to postaram się.
24 maj 21:21
Trebuh: Dzięki rozumiem, genialne 😇😇
25 maj 06:50
Mila:
Zrobię lepszy rysunek i napiszę kolejność dodatkowych linii.
25 maj 12:16
Trebuh:
Jednak nadal nie rozumiem skąd AOC ma 160
25 maj 15:30
Trebuh: Tak jakby wszystko rozumiem, ale skąd wiemy że BK to dwusieczna kąta i kąt BKS to właśnie 20
stopni?
26 maj 06:29
Trebuh: Przepraszam że tak dopytuje, ale chciałabym to dobrze zrozumieć.
26 maj 06:32
Trebuh: A dlaczego BSK ma 120 stopni? Przecież nie wiemy, że punkty B, S, O leżą na 1 prostej, bo to
jest do udowodnienia.
26 maj 16:24
Mila:
Nie podoba mi się ten sposób. Przykro mi.

26 maj 23:36
Trebuh: Tzn nie jest dobrze?
27 maj 11:04
Trebuh: A Pan chichi? Chwalił się że wie jak to zrobić.
27 maj 11:08
Mila:
Czekaj, coś się wymyśli do końca

27 maj 15:42
Mila:
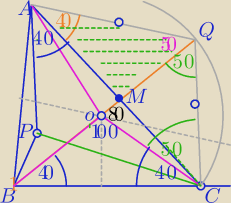
1)
O−środek okręgu opisanego na ΔABC.
|OA|=|OB|=|OC|=R
2) Rysuję okrąg opisany na ΔABC
|∡BAC|=50
o⇒|∡BOC|=100
o
3) BQ− średnica
|∡BAQ|=90
o − jako kąt wpisany w okrąg oparty na średnicy⇒|∡MAD|=40
o
ΔCOQ− Δrównoramienny, kąty przy podstawie QC : 50
,50
o
|AQ|=|QC|⇔MQ jest wysokością i dwusieczną kąta Q
4) Teraz można różnie ustalić miary kątów B i C
np.
Suma kątów przeciwległych w czworokącie wpisanym w okrąg jest równa 180
o
Zatem :
|∡B|=80
o−100
o=80
0 i |∡C|=50
o
|BC|=|AB|
===========================
27 maj 18:56
Kacper: Widzę że dyskusja trwa 🤗
Ja obecnie zajęty jestem, bo koniec roku się zbliża, jak znajdę trochę czasu to wrzucę ten
sposób z trygononetrią.
27 maj 19:26
Mila:
Cześć, właśnie chciałam zastosować trygonometrię wg Cevy, ale trudne równanie mam.
Pozdrawiam, powodzenia w ocenianiu

27 maj 20:07
Trebuh: Dziękuję za wszelką pomoc.
Dlaczego AQ=QC? Z czego to wynika?
27 maj 21:03
Mila:
∡MAQ|=40o
27 maj 21:31
Mila:
Rozważaj kąty miary kątów wpisanych.
Podałam różne informacje, masz z nich skorzystać , aby ustalić miary kątów B i C.
Jeśli nie wpadniesz na dobry pomysł, to napisz. Podpowiem.
Zacznij od najpierw ustalonych. CBQ i CAQ.
27 maj 21:41
Trebuh: Nadal nie wiem na jakiej podstawie AQB ma 50 stopni lub ACQ ma 40 stopni 😪
Jeden z nich wystarczy do wykazania tezy.
Poza tym w ogóle nie skorzystaliśmy z części danych związanych z punktem P.
28 maj 06:15
Mila:
Tak jak poprzednio:
Połączyć punkty A i S− otrzymujesz ΔASC− trójkąt równoramienny o kątach30,30,120.
ΔAOS i COS − Δ przystające cecha : bbb
dalej sama
Narysować na nowo?
28 maj 19:21
chichi:
@
Trebuh "A Pan chichi? Chwalił się że wie jak to zrobić"
Mogę wrzucić któreś ze swoich najprostszych rozwiązań tego problemu, ale jeśli nie jesteś
"obcykany" w geometrii, albo nie jesteś olimpijczykiem, to wątpię żebyś je zrozumiał, decyzja
należy do Ciebie

28 maj 21:28
an:
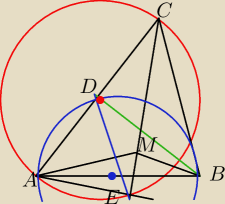
∡MAB=10
o,∡MBA=20
o,∡MCA=30
o , ∡MAC=40
o.
kreślimy prostą AE pod kątem 10
o do AB, ∡AEC=90
o
kreślimy okrąg o średnicy AC, opisany na △AEC, ∡ADB=90
o △ADE jest równoboczny
kreślimy okrąg o średnicy AB, ∡ADB=90
o
△ADB i △CDB są przystające,
tym samym trójkąt ABC jest równoramienny ∡ABC=80
o; ∡MBC=60
o
29 maj 00:07
Trebuh: Miła poproszę o ten rysunek jeśli można 🤗
Chichi jak wrzucisz to będę w stanie to ocenić, szkoda że Ty oceniasz mnie przedtem. Przy
okazji jestem dziewczyną.
an dziękuję za pomoc, mam pytanie, skąd wiemy że ADB ma 90 stopni?
29 maj 00:49
chichi:
Szkoda, że ja nikogo nie oceniłem... No, ale cóż będzie trzeba popracować nad maturą z języka
polskiego. Po pytaniu do
@an mam wątpliwości czy cokolwiek tu wstawiać. Takich zadań na
maturze na pewno nie będzie, a geometrii z forum się nie nauczysz

29 maj 05:01
Trebuh:
Nie będę przytaczać konkretnych zapisów z postów. Każdy może przeczytać i samemu ocenić.
W takim razie Tobie nie dziękuję za pomoc, bo jej wcale nie udzieliłeś.
29 maj 08:01
Mila:
Trebuh, W rozwiązaniu an :
|∡ADB|=90o jako miara kąta wpisanego w okrąg ( niebieski) opartego na średnicy AB.
29 maj 17:59
Trebuh: To zatem dlaczego punkt D jest środkiem odcinka AC? Rozumiem że zaczynamy od kreślenia
niebieskiego okręgu, a potem czerwony.
29 maj 20:14
Trebuh: Skoro kresle okrąg o średnicy AC, czyli zakładam że D jest środkiem AC, a potem pisze że ADB ma
90 stopni, to już to byłby koniec zadania przecież.
29 maj 20:20
Mila:
Poczekaj na wyjaśnienie
an .
Jeśli chodzi o moją propozycję rozwiązania to myślę, jak rozwiać Twoje wątpliwości.
Wykaż cierpliwość

29 maj 22:01
Trebuh: Dziękuję bardzo 🤗
29 maj 22:07
an: Rzeczywiście brak dowodu, że D należy do niebieskiego okręgu. Mam już dość tego rysowania
i daje opis do mojego rysunku wyżej
Oznaczmy środek niebieskiego okręgu jako G. Wówczas powstały trójkąt AGD jest podobny do
trójkąta ABC gdyż mają wspólny kąt BAC a AC=2x|AD|, oraz AB=2x|AG|, przy czym GA=GD
czyli ΔADG jest równoramienny, a ΔABC jako podobny jest również równoramienny
30 maj 00:38
Trebuh: Dziękuję, już zaczynam analizować 😇
30 maj 10:38
Trebuh:
an dlaczego GA=GD?
1 cze 08:59
Trebuh: Bo skoro zakładam że tak jest, to znaczy że zakładam że punkt D należy do niebieskiego, a to
mieliśmy pokazać
1 cze 09:00
Trebuh: Mila, dlaczego BD jest równoległa do EP'?
1 cze 19:14
Mila:
Trebuh
23 maj 18:31
albo
27 maj 18:56
Którą wersję uzupełnić?
( a może sama już wyjaśniłaś wątpliwości).
3 cze 16:21
Trebuh: Myślę że bardziej tę z 27 maja, była jeszcze inna, ale chyba zniknęła 😅
4 cze 20:33
Mila:
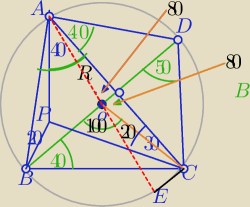
1) Rysuję ΔABC, odcinki jak w treści i okrąg opisany.
2) Kreślę średnicę BD
∡BAD, ∡BCD− kąty proste jako wpisane oparte na średnicy
|∡BOC|=2*50
o=100 jako kąt środkowy oparty na cięciwie BC tak jak kąt BAC wpisany w okrąg
|∡DOC|=80
o jako przyległy do ∡BOC
|∡BDC|=50 jako kąt wpisany oparty na BC
3) rysuję średnicę AE, ∡EOC=20
o to ∡EAC i ∡OCA mają po 10
o ⇒
|∡AOD|=80
o
Teraz dokończyć można w różny sposób
np.
| | 1 | |
kąt wpisany ABC= |
| *160o =80o |
| | 2 | |
∡BCA=180
o−80
o−50
o=50
o.
|BC|=|BA|
4 cze 22:53
Trebuh:
Bardzo dziękuję za rysunek.
Jak zwykle mam pytanie 🤦♂️ Skąd wiemy że kąt EOC ma 20 stopni?
5 cze 07:19
Trebuh: Nadal nie rozumiem dlaczego korzystamy z faktu że BD i AC są prostopadłe
10 cze 08:10
Trebuh: Dziękuję za konstruktywną odpowiedź.
10 cze 15:19
Mila:
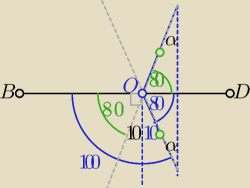
Może kąty wierzchołkowe i przyległe ?
Szkic.
Trudno jest mi to umieścić na rysunku typu 22:53 , bo jest mało miejsca w polu na grafikę.
Jeśli to nie wyjaśni Twoich wątpliwości, to podam inny sposób albo narysuję w geogebrze
( jeśli lepiej opanuję to rysowanie za pomocą geogebry).
Czy dowód z zastosowaniem trygonometrii zrobiłaś?
10 cze 16:11
Trebuh: Ten dowód z linku mi się podoba z trygonometrii.
Nanoszę te rzeczy, które mam teraz od Ciebie i mam nadzieję, że już wszystko będzie jasne 🤦♂️
10 cze 19:53
Mila:
1)
Narysuj duży rysunek. Wyjdzie.
Wszystko tutaj zapętla się i mnie wydawały się pewne miary kątów oczywiste.
2)Chodzi Ci o dowód z konkursu 1996 r. z amerykańskiej olimpiady?
10 cze 20:47
 Przygotowuje sie do konkursu z geometri i polecenie jest takie
Pokaz ze trojkat ABC jest rownoramienny wykorzystujac jedynie zasady geometri syntetycznej (bez
uzycia metod algebrainczych). Prosze o odpowiedz albo naprowadzenie
Przygotowuje sie do konkursu z geometri i polecenie jest takie
Pokaz ze trojkat ABC jest rownoramienny wykorzystujac jedynie zasady geometri syntetycznej (bez
uzycia metod algebrainczych). Prosze o odpowiedz albo naprowadzenie


 Ale wtedy na rys. powinno być tak
A tak nie jest
więc coś nie ... halo
Ale wtedy na rys. powinno być tak
A tak nie jest
więc coś nie ... halo 

 Ja z trygonometrii mam pomysł, ale wiadomo, że najładniejsze są rozwiązania syntetyczne
Ja z trygonometrii mam pomysł, ale wiadomo, że najładniejsze są rozwiązania syntetyczne 

 Podpowiedź
1) rysunek
2)
O − punkt przecięcia symetralnych boków Δ ( środek okręgu opisanego na ΔABC)
ΔAKB− Δrównoramienny (20,20 ,140)
ΔΔASC −Δrównoramienny (30, 30,120)
Podpowiedź
1) rysunek
2)
O − punkt przecięcia symetralnych boków Δ ( środek okręgu opisanego na ΔABC)
ΔAKB− Δrównoramienny (20,20 ,140)
ΔΔASC −Δrównoramienny (30, 30,120)



 1)
O−środek okręgu opisanego na ΔABC.
|OA|=|OB|=|OC|=R
2) Rysuję okrąg opisany na ΔABC
|∡BAC|=50o⇒|∡BOC|=100o
3) BQ− średnica
|∡BAQ|=90o − jako kąt wpisany w okrąg oparty na średnicy⇒|∡MAD|=40o
ΔCOQ− Δrównoramienny, kąty przy podstawie QC : 50,50o
|AQ|=|QC|⇔MQ jest wysokością i dwusieczną kąta Q
4) Teraz można różnie ustalić miary kątów B i C
np.
Suma kątów przeciwległych w czworokącie wpisanym w okrąg jest równa 180o
Zatem :
|∡B|=80o−100o=800 i |∡C|=50o
|BC|=|AB|
===========================
1)
O−środek okręgu opisanego na ΔABC.
|OA|=|OB|=|OC|=R
2) Rysuję okrąg opisany na ΔABC
|∡BAC|=50o⇒|∡BOC|=100o
3) BQ− średnica
|∡BAQ|=90o − jako kąt wpisany w okrąg oparty na średnicy⇒|∡MAD|=40o
ΔCOQ− Δrównoramienny, kąty przy podstawie QC : 50,50o
|AQ|=|QC|⇔MQ jest wysokością i dwusieczną kąta Q
4) Teraz można różnie ustalić miary kątów B i C
np.
Suma kątów przeciwległych w czworokącie wpisanym w okrąg jest równa 180o
Zatem :
|∡B|=80o−100o=800 i |∡C|=50o
|BC|=|AB|
===========================


 ∡MAB=10o,∡MBA=20o,∡MCA=30o , ∡MAC=40o.
kreślimy prostą AE pod kątem 10o do AB, ∡AEC=90o
kreślimy okrąg o średnicy AC, opisany na △AEC, ∡ADB=90o △ADE jest równoboczny
kreślimy okrąg o średnicy AB, ∡ADB=90o
△ADB i △CDB są przystające,
tym samym trójkąt ABC jest równoramienny ∡ABC=80o; ∡MBC=60o
∡MAB=10o,∡MBA=20o,∡MCA=30o , ∡MAC=40o.
kreślimy prostą AE pod kątem 10o do AB, ∡AEC=90o
kreślimy okrąg o średnicy AC, opisany na △AEC, ∡ADB=90o △ADE jest równoboczny
kreślimy okrąg o średnicy AB, ∡ADB=90o
△ADB i △CDB są przystające,
tym samym trójkąt ABC jest równoramienny ∡ABC=80o; ∡MBC=60o


 1) Rysuję ΔABC, odcinki jak w treści i okrąg opisany.
2) Kreślę średnicę BD
∡BAD, ∡BCD− kąty proste jako wpisane oparte na średnicy
|∡BOC|=2*50o=100 jako kąt środkowy oparty na cięciwie BC tak jak kąt BAC wpisany w okrąg
|∡DOC|=80o jako przyległy do ∡BOC
|∡BDC|=50 jako kąt wpisany oparty na BC
3) rysuję średnicę AE, ∡EOC=20o to ∡EAC i ∡OCA mają po 10o ⇒
|∡AOD|=80o
Teraz dokończyć można w różny sposób
np.
1) Rysuję ΔABC, odcinki jak w treści i okrąg opisany.
2) Kreślę średnicę BD
∡BAD, ∡BCD− kąty proste jako wpisane oparte na średnicy
|∡BOC|=2*50o=100 jako kąt środkowy oparty na cięciwie BC tak jak kąt BAC wpisany w okrąg
|∡DOC|=80o jako przyległy do ∡BOC
|∡BDC|=50 jako kąt wpisany oparty na BC
3) rysuję średnicę AE, ∡EOC=20o to ∡EAC i ∡OCA mają po 10o ⇒
|∡AOD|=80o
Teraz dokończyć można w różny sposób
np.
 Może kąty wierzchołkowe i przyległe ?
Szkic.
Trudno jest mi to umieścić na rysunku typu 22:53 , bo jest mało miejsca w polu na grafikę.
Jeśli to nie wyjaśni Twoich wątpliwości, to podam inny sposób albo narysuję w geogebrze
( jeśli lepiej opanuję to rysowanie za pomocą geogebry).
Czy dowód z zastosowaniem trygonometrii zrobiłaś?
Może kąty wierzchołkowe i przyległe ?
Szkic.
Trudno jest mi to umieścić na rysunku typu 22:53 , bo jest mało miejsca w polu na grafikę.
Jeśli to nie wyjaśni Twoich wątpliwości, to podam inny sposób albo narysuję w geogebrze
( jeśli lepiej opanuję to rysowanie za pomocą geogebry).
Czy dowód z zastosowaniem trygonometrii zrobiłaś?