Geometria analityczna Edward : Prosta l , na której leży punkt P = ( ) 8, 2 , tworzy z dodatnimi półosiami układu współrzędnych trójkąt prostokątny o polu równym 36. Wyznacz równanie prostej l .

PATMAT16: Ja bym to zrobił tak: Prosta przechodząca przez punkt P(8;2) wyraża się równaniem: y=a(x−x₀)+b y=a(x−8)+2 Wyznaczamy punkt przecięcia z osią: a) OX b) OY 0=ax−8a+2 y=a(0−8)+2 Wyznaczamy x: y=−8a+2 −ax=−8a+2 /:(−a)

	2
x=8−
	a

Wzór na pole trójkąta:

	b*h		b*h		2
P=		⇒ 36=		, gdzie b=x=8−		h=y=−8a+2}
	2		2		a

Wystarczy teraz podstawić do wzoru i obliczamy:

b*h
	=36 /*2
2

b*h=72

	2
(8−		)(−8a+2)=72
	a

	4
−64a+16+16−		=72
	a

	4
−64a+32−		=72 /*a
	a

−64a²+32a−4=72a −64a²−40a−4=0 /:(−4) 16a²−10a+1=0 Δ=(−10)²−4*16=100−64=36 / √ √Δ=6

	10−6		4		1
a1=		=		=
	2*16		32		8

	10+6		16		1
a2=		=		=
	32		32		2

Będą dwie takie proste:

	1
y=		x+2
	8

	1
y=		x+2
	2

PATMAT16: Tam jest +10a. Wtedy

	1
a1=−
	8

	1
a2=−
	2

PATMAT16: Przecięcie z osią OY to: b=y=−8a+2

	1
b1=−8*(−		)+2=1+2=3
	8

	1
b2=−8*(−		)+2=4+2=6
	2

Zatem:

	1
y1=−		+3
	8

	1
y2=−		+6
	2

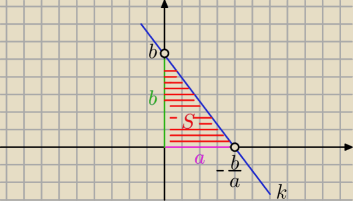
Eta: Z równania odcinkowego prostej

	x		y
k:		+		=1 2S=ab = 72 i P=(8,2) ∊k
	a		b

===========

	8		2
		+		=1 /*ab ⇒ 4b+a=36 i ab=72
	a		b

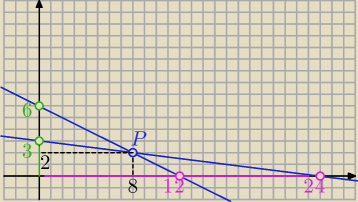
(36−4b)*b=72 / :4 ⇒ b²−9b+18=0 to (b−6)(b−3)=0 b=6 v b=3 to a= 12 v a=24 w postaci odcinkowej

	x		y		x		y
k:		+		=1 lub k:		+		=1
	12		6		24		3

==========================

	b
w postaci kierunkowej: k: y= −		x +b
	a

============

	1		1
k: y= −		x +6 lub k : y= −		x+3
	2		8

============================

Eta: