Dla jakiego m funkcja g osiąga ekstremum w tym samym punkcie co funkcja f Nova: Dane są funkcje f(x)= 2x² −8x + 1 i g(x)= m² x² + (4m + 1)x + 3, gdzie m≠0. Dla jakiego m funkcja g osiąga ekstremum lokalne w tym samym punkcie, co funkcja f?

chichi: Pochode umiesz liczyć?

chichi: Pochodne*

Nova: Tak, wyliczyłem że funkcja f osiąga minimum dla x=2. W jaki sposób teraz wyliczyć m?

PATMAT16: Teraz obliczasz f(2), następnie wartość tej funkcji wstawiasz za g(x), a za 'x' podstawiasz 2.

Nova: Otrzymałem równanie 4m² + 8m + 12 = 0. △=−128

Nova: Zapomniałem podzielić równania przez 4, ale i tak △ wychodzi ujemna

Nova: W jaki sposób wyliczyć z tego m?

Nova: Czy ktoś potrafiłby rozpisać to zadanie, żebym zobaczył gdzie robię błąd?

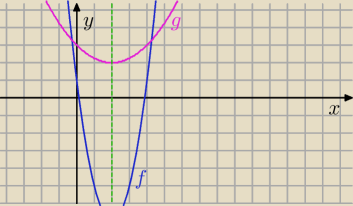
chichi: Zauważmy, że dla m ≠ 0 wykresami f oraz g są parabole, które swoje ekstrema osiągają w wierzchołku, zatem jeśli f osiąga ekstremum w punkcie x = 2, to g musi też tam osiagać ekstremum czyli f i g muszą mieć taką samą odcięta wierzchołka A teraz podchwytliwie (a może i nie) co z przypadkiem liniowym?

chichi:

	1
Dla m = −
	2

Nova: Z założenia jest m≠0 więc nie rozważamy przypadku liniowego. Bardzo dziękuję za pomoc!

chichi: Tak. Na zdrowie