Równanie okręgu, geometria analityczna
Algorytm:
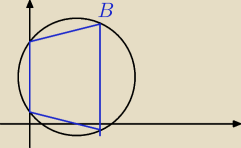
Trapez o podstawach AB i CD jest wpisany w okrąg o równaniu x
2+y
2+5=6(x+6)
Jego krótsza podstawa leży na osi OY, a B = (5,6). Wyznacz pozostałe wierzchołki trapezu, a
nastepnie oblicz jego pole i obwód.
Po przekształceniu równania okręgu do:
(x−3)
2+(y−3)
2 =
√13
Skoro w okrąg można wpisać tylko trapez równoramienny to mogę wziąć punkty analizując z
wykresu?
27 kwi 01:08
Algorytm: (x−3)2+(y−3)2 = 13
27 kwi 01:09
chichi:
x2 + y2 + 5 = 6(x + 6)
x2 − 6x + 9 + y2 = 40
(x − 3)2 + y2 = 40
Średnio mi to przypomina równanie Twojego okręgu.
Jak i będziesz teraz konstruował cyrklem 2√10 żeby odczytywać punkty? Proszę cię.
Rób analitycznie...
27 kwi 01:18
Algorytm: Dobra, dzięki!
27 kwi 01:41
janek191:
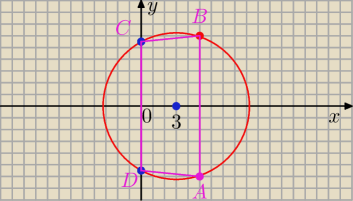
(x − 3)
2 + y
2 = 40
x = 5
2
2 + y
2 = 40
y
2 = 36
y = − 6
A = ( 5, −6)
=========
x = 0
9 + y
2 = 40
y
2 = 31
y = −
√31 lub y =
√31
c = ( 0,
√31) D = ( 0, −
√31)
============ ===============
27 kwi 01:42
Algorytm: zrobiłem literówkę w równaniu okręgu xd
x2+y2+5=6(x+y)
27 kwi 01:42
Algorytm: Ale dzięki, już wyłapałem xd
27 kwi 01:42