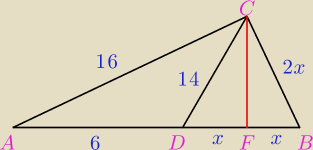
 Punkt D leży na boku AB trójkąta ABC oraz |AC|=16, |AD|=6, |CD|=14 i |BC|=|BD|
Oblicz obwód trójkąta ABC
Jak poprowadzę wysokość, to podobieństwo trójkątów FDC i FAC względem kąta prostego:
Dlaczego nie da się tego zrobić z podobieństwa trójkątów:
Punkt D leży na boku AB trójkąta ABC oraz |AC|=16, |AD|=6, |CD|=14 i |BC|=|BD|
Oblicz obwód trójkąta ABC
Jak poprowadzę wysokość, to podobieństwo trójkątów FDC i FAC względem kąta prostego:
Dlaczego nie da się tego zrobić z podobieństwa trójkątów:
| x | x+6 | ||
= | |||
| 14 | 16 |
 Prawidłowy wynik to 120
Prawidłowy wynik to 120

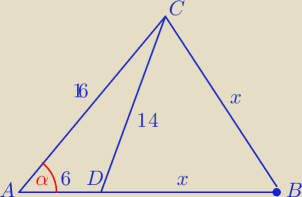 Tw. kosinusów.
Tw. kosinusów.
| 25 | ||
cos α = | ||
| 48 |


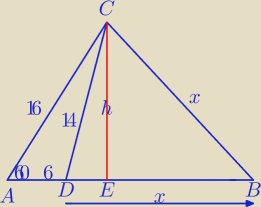 II sposób
Pole ΔADC:
1)
II sposób
Pole ΔADC:
1)
| 6+14+16 | ||
p= | =18 | |
| 2 |
| 1 | ||
24√3= | *6*16 sinα | |
| 2 |
| √3 | ||
sinα= | ⇔α=60o | |
| 2 |


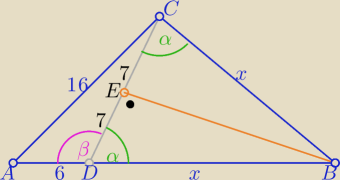
| 7 | ||
cosα= | i cosβ= cos(180o−α)=−cosα | |
| x |
| 36+196−256 | 1 | 1 | ||||
cosβ= | = − | ⇒ cosα= | ||||
| 2*6*14 | 7 | 7 |
| 7 | 1 | |||
to: | = | ⇒ x=49 | ||
| x | 7 |