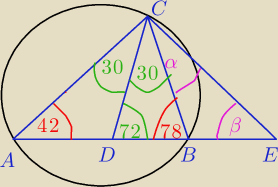
Planimetria PATMAT16: Trochę mi rysunek nie wyszedł, ale prosta EC nie przecina okręgu w dwóch punktach, tylko jest to styczna, a punktem styczności jest C Odcinek CD jest zawarty w dwusiecznej kąta ACB. Kąty trójkąta ABC mają miary: |∡CAB|=42*, |∡ABC|=78* Styczna do okręgu opisanego na tym trójkącie w punkcie C przecina prostą AB w punkcie E (zobacz rysunek) OBLICZ,ILE MA KAŻDY Z KĄTÓW TRÓJKĄTA CDE Kąty na czerwono, to te które podane są w zadaniu Kąty na zielono, znalezione przeze mnie Kąty na różowo, to kąty brakujące do podania odpowiedzi. Nie mam pomysłu na znalezienie tych kątów Może zachodzą tu zależności dla któregoś z kątów których nie widzę

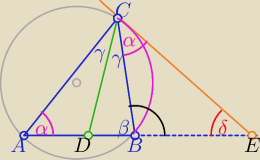Eta: α=42^o ∡BCE =α − jako kąt dopisany oparty na łuku BC β=78^o to 2γ=60^o ⇒γ=30^o zatem ∡ z= α+2γ = 102^o −− jako kąt zewnętrzny ΔABC więc ∡δ=36^o to ∡CDE=.............