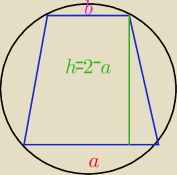
Rozpatrujemy wszystkie trapezy równoramienne, w które można wpisać okręg, spełniające warunek:
suma długości dłuższej podstawy "a" i wysokości trapezu jest równa 2.
a) Wyznacz wszystkie wartości "a", dla których istnieje trapez o podanych własnościach.
b)Wykaż, że obwód L takiego trapezu, jako funkcja długości "a" dłuższej podstawy trapezu,
| 4a2−8a+8 | ||
wyraża się wzorem L(a)= | ||
| a |
