Czworokąt ABCD jest wpisany w okrąg. Monika04: Czworokąt ABCD jest wpisany w okrąg. Proste AB i CD przecinają się w punkcie K, a proste BC i AD − w punkcie L. Miary kątów BKC i CLD są równe odpowiednio 45° i 25°. Wyznacz miary kątów czworokąta ABCD. Suma kątów: α + β + γ + δ = 360st Kąty α, δ i 45st dają 180st, ponieważ są to kąty trójkąta AKC Kąty α, β i 25st dają 180st, ponieważ są to kąty trójkąta ALB Z tablic wiem, że kąty czworokąta wpisanego w okrąg α + γ = β + δ Na podstawie tego chce obliczyć kąty: α + δ + 45st = 180st a = 135st − δ β + 135st − δ + 25st = 180st β = 20st + δ α + γ = β + δ 135st − δ + γ = 20st + δ + δ γ = −115st + δ α + β + γ + δ = 360st 135st − δ + δ + 20st − 115st + δ + δ = 360st 2δ = 360st δ = 180st Kąt δ nie może wynosić 180st, jest to niemożliwe, niestety nie wiem gdzie zrobiłam błąd, czy jakaś miła duszyczka mogłaby mi pomóc go dostrzec

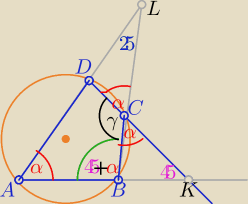
Eta: α kąty wierzchołkowe w trójkątach BKC i DLC γ=180^o−α to ∡BAD= α ( bo czworokąt wpisany w okrąg ∡ABC= 45^o+α −− jako kąt zewnętrzny trójkąta BKC zatem w ΔABL : α+45^o+α+25^o=180^o ⇒ α=55^o teraz dokończ...........