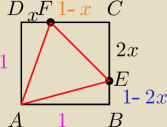
Optymalizacja PATMAT16: Proszę bardzo o sprawdzenie. Z góry dziękuję. Bok kwadratu ABCD ma długość 1. Na bokach BC i CD wybrano odpowiednio punkty E i F umieszczone tak, by |CE|=2|DF|. Oblicz wartość x=|DF|, dla której pole trójkąta AEF jest najmniejsze. Czy mogę to zrobić tak? (dla mnie sposób najbardziej zrozumiały. Wiedząc, że bok kwadratu wynosi 1, jego pole jest też równe 1. Założenia: 1)x>0 2)1−x>0 ⇔ −x>−1 /*(−1) x<1 3)1−2x>0 ⇔ −2x>−1 /:(−2) x<¹₂ x∊(0;¹₂) Teraz będę odejmował pola trzech trójkątów (ΔABE,ΔADF,ΔFCE) od pola kwadratu ABCD.

	1		1		1
P=1−		(1−2x)−		2x(1−x)−		x
	2		2		2

	1		1
P=1−		+x−x(1−x)−		x
	2		2

	1		1
P=1−		+x−x+x2−		x
	2		2

	1		1
P=x2−		x+
	2		2

Funkcja kwadratowa osiąga minimum w wierzchołku, więc:

	−b		1
p=		⇒ p=
	2a		4

	1
|DF|=xmax=p=
	4

PATMAT16:

	1
|DF|=xmin=p=		. Pomyłka
	4

wredulus_pospolitus: rozwiązanie dobre ... bym się tylko ewentualnie zastanowił nad: x ∊ <0 ; 1/2> <−−− w końcu wierzchołki są także częścią boków.

PATMAT16: Dlaczego przedział domknięty?

PATMAT16: Jeżeli x=0 to nie ma kwadratu

PATMAT16: A dobra jednak jest

PATMAT16: Już z przyzwyczajenia wziąłem, że x≠0

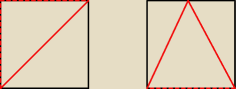wredulus_pospolitus: po lewej − x=0

	1
po prawej − x =
	2

PATMAT16: Ale chwila. Jednak nie rozumiem haha. Oblicz wartość x=|DF|, dla której pole trójkąta AEF jest najmniejsze.

	1
|DF|=x=
	4

Czyli nie może być przedziału domkniętego

PATMAT16: Bo wtedy |DF| może być równe 0

wredulus_pospolitus: no i F = D Wierzchołek D jest częścią boku CD, obrano punkt F będący w wierzchołku D. Nie zmienia to samego zdania i podejrzewam, że sprawdzający nawet by się nie zwrócił na to uwagi. Co więcej − możliwe, że byłyby zdania podzielone co do tego, czy przedział powinien być domknięty, czy też nie. Ja osobiście bym domknął, ale rozumiem jeżeli by ktoś twierdził, że przedziały powinny być otwarte.

PATMAT16: To jest zadanie maturalne z maja 2010 roku za 4 punkty. Jak teraz sprawdziłem w odpowiedziach, to nie domknęli przedziału. Dziękuję ci jeszcze raz za sprawdzenie zadania.