Prawdopodobieństwo Algorytm: W pierwszej urnie jest 5 białych i 3czerwonych kul, w drugiej 6 białych i 6 czerwonych kul. Losujemy 1 kulę z pierwszej urny i przekładamy do drugiej, z drugiej urny losujemy 1 kulę i przekładamy do pierwszej. Z pierwszej urny losujemy 2 kule. Jakie jest prawdopodobieństwo, że obie wylosowane kule są czerwone?

wredulus_pospolitus: A₁ −−− losujemy białą, później białą, później dwie czerwone A₂ −−− losujemy czerwoną, później białą, później dwie czerwone A₃ −−− losujemy czerwoną, później czerwoną, później dwie czerwone A₄ −−− losujemy białą, później czerwoną, później dwie czerwone P(A) = P(A₁) + P(A₂) + P(A₃) + P(A₄) LICZYSZ

Algorytm: Narysowałem drzewko 3 piętrowe z wydarzeniami przerzucenia losowej kuli z jednej do drugiej. Mając na końcu po tych przekładaniach kul (przed losowaniem 2 kul) stan 1 urny jest taki 1) Białych: 5 Czerwonych: 3 2) Białych: 4 Czerwonych: 4 3) Białych: 6 Czerwonych: 2 4) Białych: 5 Czerwonych: 3

	3		2		6
I miałem tak, że z pierwszego wypadku mam:		*		=		;
	8		8		56

	12
z drugiego:		;
	56

	2
z trzeciego:		;
	56

	6
z czwartego:
	56

i mam zły wynik

I'm back: Co Ty zrobiłeś?

Algorytm: No zrobiłem sobie 4 przypadki 1 urny po przekładaniach kul.

I'm back: No Okey. A czemu nie uwzględniasz Prawdopodobieństwa 'dotarcia' do danej sytuacji w urnie nr 1?

I'm back: Patrz co napisałem na początku, w pierwszej odpowiedzi

Algorytm: Ale właśnie uwzględniam. Z 1 urny białą przekładam do 2 urny, następnie wylosowało mi kule białą z drugiej i przekładam do pierwszej.

I'm back: Ale gdzie W OBLICZENIACH to uwzględniasz? Prawdopodobieństwo przełożenia czerwonej do drugie urny, a później białej do urny 1, aby w końcu wylosowac dwie czerwone z drugiej

I'm back: Z pierwszej* a nie z drugiej

wredulus_pospolitus: Napisałeś, że narysowałeś drzewko −−− widać, nie zrobiłeś pełnego drzewka

Algorytm: I'm back, Ale ja losuje dwie czerwone z pierwszej urny wredulus−pospolitus, w jakim sensie?

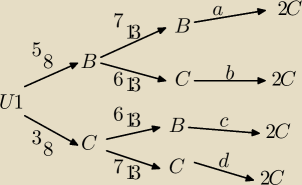
wredulus_pospolitus: narysowałem NIEPEŁNE drzewo (nie narysowałem wszystkich innych opcji wylosowania z pierwszej urny w ostatnim kroku ... za dużo tego, a i tak nas to nie obchodzi) a,b,c,d to jest to co policzyłeś ... ale nie uwzględniłeś tych prawdopodobieństw, które doprowadzały do sytuacji wyliczanych i w końcowym etapie

wredulus_pospolitus: Musisz to uwzględnić Przykład: W 1 urnie mamy 1 białą i 1 czerwoną, losujemy jedną kulę i przekładamy do drugiej W 2 urnie mamy 1 białą i 0 czerwonych, losujemy jedną kulę i przekładamy do trzeciej W 3 urnie mamy 0 białych i 1 czerwoną, losujemy jedną kulę − oblicz Pr, że będzie to kula biała więc będziesz liczył:

	1		1		1		1		1
P(A) =		*1*		+		*		*
	2		2		2		2		2

czyli wylosowanie: biała −> biała −> biała + czerwona −> biała −> biała (pozostałe opcje pomijam, bo nie wylosowanie w drugiej urnie białej powoduje brak białych w trzeciej urnie.

wredulus_pospolitus: PS. −−− oba nikt to 'mła' jedno to komórka, drugie to laptop

Algorytm: Aha, no tak, racja XD, zapomniałem pomnożyć, dziękuję bardzo za wytłumaczenie!